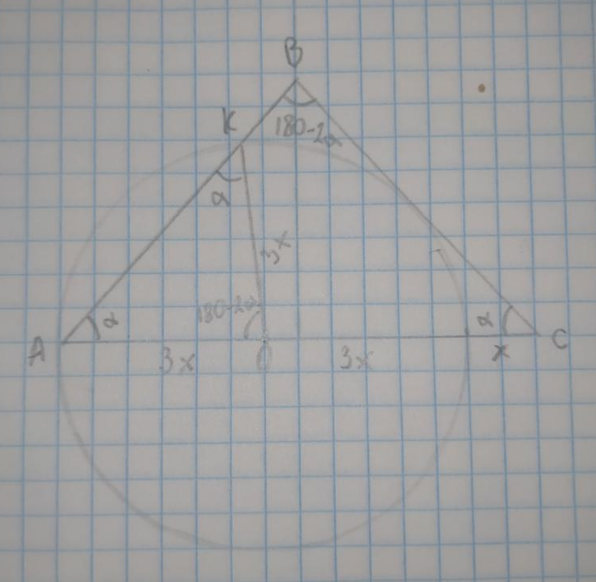
Точка О делит основание АС равнобедренного треугольника АВС в отношении 3:4 считая от вершины А. Окружность с центром в точке О и радиусом ОА касается стороны ВС. В каком отношении эта окружность делит сторону АВ?

1 ответ

Посмотреть ответы

Ответ, проверен экспертом

d.scherbetov

Точка К - точка пересечения прямой АВ с окружностью, провела к ней отрезок ОК=АО=3х, т.к. является радиусом окружности. Получается, что треугольник АКО равнобедренный с углами а, а, 180°-2а.
У треугольника АВС и АКО угол а совпадает, тогда угол АВС имеет углы а, а, 180°-2а. Соответственно они подобны по трем углам.
Тогда сторона КО подобна стороне АВ. k - коэффициент подобия. Тогда АВ=КО*k=3xk.
Сторона КА подобна АС, тогда АС=КА*k, следовательно КА=АС/k=7x/k
KB=AB-KA=3xk-7x/k=(3xk²-7x)/k
Находим отношение КВ к КА:
((3хk²-7x)/k)/(7x/k)=(3k²-7)/7

Хороший ответ

30 января 2023 07:32

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Спичечный рак ползет вверх . Переложи три спички так ято бы он пополз вниз.... Пусть М – множество всех шестнадцатизначных натуральных чисел, для каждого из которых выполняются два условия: оно является квадратом целого числа и в... 4/5 8/25 1/4 3/50 17/20 представьте в виде десятичной дроби... Смешали некоторое количество 13-процентного раствора некоторого вещества с таким же количеством 17–процентного раствора этого вещества.Сколько процент... Коля стёр некоторые цифры в примере на доске и написал вместо них буквы. Вместо одинаковых цифр он написал одинаковые буквы, а вместо разных цифр-разн...