В треугольнике MNK угол M=a, угол К=B, сторона NK=7см,NP-высота. Найдите MP

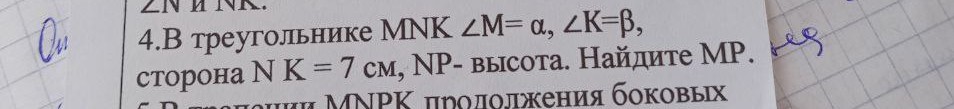
Для решения задачи нам понадобятся тригонометрические соотношения для прямоугольных треугольников. Используя эти соотношения, мы можем найти длину стороны MP, зная углы и стороны треугольника MNK.

Из условия задачи мы знаем, что сторона NK равна 7 см, а NP является высотой треугольника, проходящей из вершины N к стороне MK. Обозначим длину стороны MK через x.

Зная, что угол М равен a, мы можем записать соотношение тангенса для прямоугольного треугольника MNP:

tan(a) = NP/MP

Решая это уравнение относительно MP, получаем:

MP = NP/tan(a)

Теперь нам нужно найти длину высоты NP. Для этого мы можем использовать соотношение между сторонами и углами треугольника MNK:

tan(B) = NP/MK

Так как сторона MK равна x, мы можем выразить NP через x:

NP = x * tan(B)

Нам также известно, что сторона NK равна 7 см. Используя теорему Пифагора для прямоугольного треугольника NKM, мы можем найти длину стороны MK:

MK^2 = NK^2 - NP^2

x^2 = 7^2 - (x * tan(B))^2

Решая это уравнение относительно x, получаем:

x = 7 / sqrt(1 + tan(B)^2)

Теперь мы можем подставить найденные значения NP и x в формулу для MP:

MP = NP / tan(a) = x * tan(B) / tan(a) = (7 / sqrt(1 + tan(B)^2)) * tan(B) / tan(a)

Таким образом, длина стороны MP равна (7 / sqrt(1 + tan(B)^2)) * tan(B) / tan(a) см.