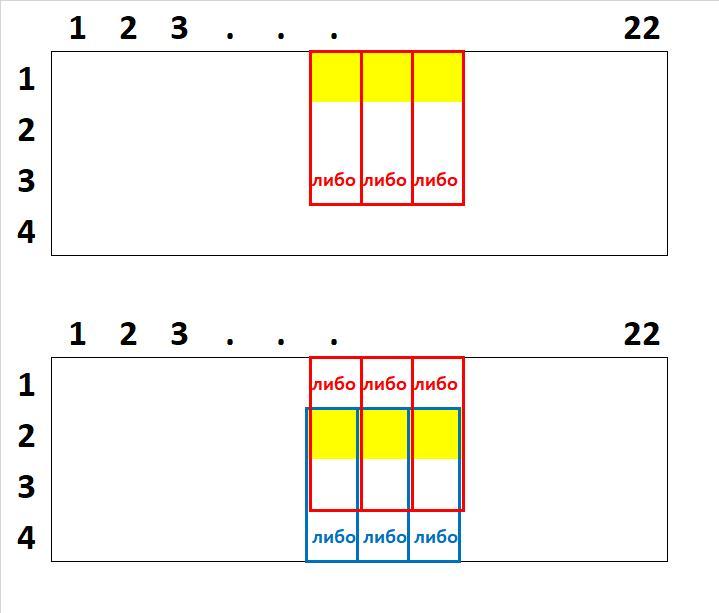
Дан клетчатый прямоугольник высоты 4 и ширины 22. Вася красит какой-тогоризонтальный прямоугольник 1×3 клетки, а Петя красит какой-то вертикальныйпрямоугольник 3×1 клетки. Найдите вероятность того, что хотя бы одна клетка будет покрашена дважды.

1 ответ

Посмотреть ответы

Megamozg

2205

Пусть, горизонтальный прямоугольник уже размещен. Тогда, искомая вероятность - вероятность того, что вертикальный прямоугольник будет пересекать горизонтальный. Заметим, что пересечение возможно только в одной клетке.
Рассмотрим две ситуации.
1. Горизонтальный прямоугольник лежит в крайней (верхней или нижней) строке. Так как всего строк 4, то это может произойти с вероятностью $\dfrac =\dfrac$ . Найдем общее число возможных расположений вертикального прямоугольника и число расположений, при которых он пересекается с горизонтальным.
Так как высота вертикального прямоугольника 3, а высота исходного прямоугольника 4, то в каждом столбце вертикальный прямоугольник моет располагаться двумя способами. Таким образом, общее число расположений вертикального прямоугольника равно $2\cdot22=44$ .
Вертикальный прямоугольник будет пересекаться с горизонтальным в 3 случаях: если он будет располагаться в одном из столбцов, через которые проходит горизонтальный прямоугольник и примыкать к соответствующей крайней строке. Значит, число расположений вертикального прямоугольника, при которых он пересекается с горизонтальным, равно 3.
Учитывая вероятность появления этой ситуации, получим, что пересечение в этой ситуации происходит с вероятностью $\dfrac \cdot\dfrac$ .
2. Горизонтальный прямоугольник не лежит в крайней строке. Таких строк тоже 2, значит произойти это может также с вероятностью $\dfrac =\dfrac$ .
Общее число расположений вертикального прямоугольника по-прежнему равно $2\cdot22=44$ .
Вертикальный прямоугольник будет пересекаться с горизонтальным, если он будет располагаться в одном из столбцов, через которые проходит горизонтальный прямоугольник, причем располагаться в конкретном столбце он может любым из двух возможных способов. Значит, число расположений вертикального прямоугольника, при которых он пересекается с горизонтальным, равно $3\cdot2=6$ .
Учитывая вероятность появления этой ситуации, получим, что пересечение в этой ситуации происходит с вероятностью $\dfrac \cdot\dfrac$ .
Рассмотренные ситуации не совместны, так как горизонтальный прямоугольник не может располагаться в двух строках одновременно. Значит, соответствующие вероятности необходимо складывать:
$P(A)=\dfrac \cdot\dfrac +\dfrac \cdot\dfrac=\dfrac \cdot\dfrac=\dfrac$
Ответ: 9/88

Хороший ответ

3 апреля 2023 19:43

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Какое число находится на второй позиции?... Какое количество секунд соответствует одному часу?... Сделай краткую запись и реши задачу: Два куска ткани стоят 360 тенге. В 1 куске 5 м ткани, во 2 куске 4м. Сколько стоит каждый кусок?... Как разделить 36 на 2 столбиком... найди ответ, используя пример-помощник: а)58*8=464 б)74*5=370 58*9= 74*4=...