Помогите, пожалуйста, с решением и с грамотным оформлением.Логарифм в квадрате числа x по основанию 3 меньше единицы.

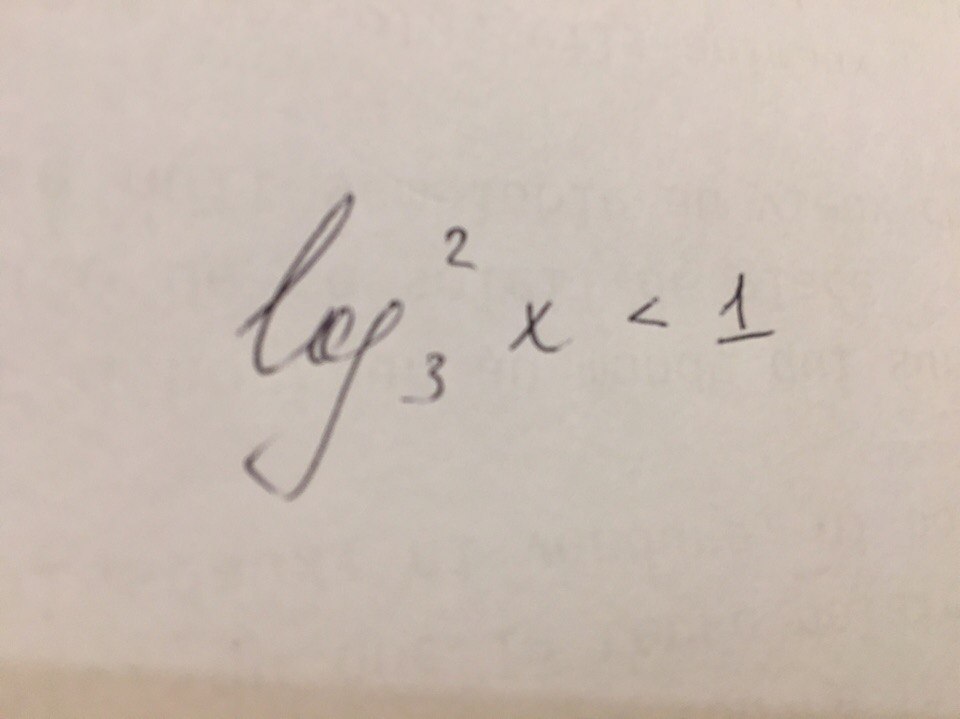
1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
x∈(1/3; 3)
Объяснение:
Дано неравенство: log²₃x<1.
Область допустимых значений: x>0 ⇒ x∈(0; +∞).
log²₃x<1 ⇔ -1<log₃x<1 ⇔ 3⁻¹<x<3¹ ⇔ 1/3<x<3 ⇔ x∈(1/3; 3)⊂(0; +∞).

Хороший ответ

3 апреля 2023 19:50

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

задана функция f (x). Выясните возрастает или убывает функция на тему заданных интервалах: (0:1); (3;4); ... Решить уравнение √x=10... 10·2/5= сколько будет?... Какие четные , какие нечетные функции 1)y=2x^4 2) y=3x^5 3) y=x^2+3 4) y=x^3-2 5)y=x^-4 6) y=x^-3 7)y=x^4+x^2 8)y=x^3 + x^5 9) y=x^2 - x + 1 10) y=1/x... Постройте график зависимости y равно x при x больше или равно 1 1 при x меньше 1...