Докажите что , если медиана треугольника равна половине стороны , к которой она проведена , то треугольник прямоугольный.

1 ответ

Посмотреть ответы

Megamozg

2205

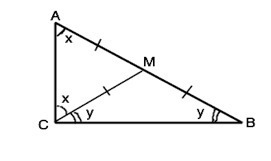
Пусть в ∆ АВС отрезок СМ - медиана и по условию СМ=АМ=ВМ. Тогда ∆ АМС и ∆ ВМС - равнобедренные с равными углами при основаниях. Примем ∠МАС=∠МСА=х, и ∠МСВ=МВС =у
Сумма углов треугольника 180° ⇒ 2х+2у=180° ⇒ х+у=90°. Тогда ∠АСВ=х+у=90°. ⇒ ∆ АВС - прямоугольный. Доказано.

Хороший ответ

3 апреля 2023 20:25

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Какое отображение плоскости называется параллельным переносом на данный вектор ?... Помогите!!! Средние линии треугольника относятся как 2 :2: 4 ,а периметр треугольника равен 45 см. найдите сторону треугольника !!!даю много баллов ,... Найдите площадь кольца, считая стороны квадратных клеток равными 1, в ответе запишите s/п... Большая боковая сторона прямоугольной трапеции равна 12√2 см, а острый угол - 45°, найдите площадь трапеции, если известно, что в трапецию можно вписа... Какая фигура называется симметричной относительно данной прямой?...