С помощью циркуля и линейки постройте биссектрису угла треугольника, и докажите что это биссектриса

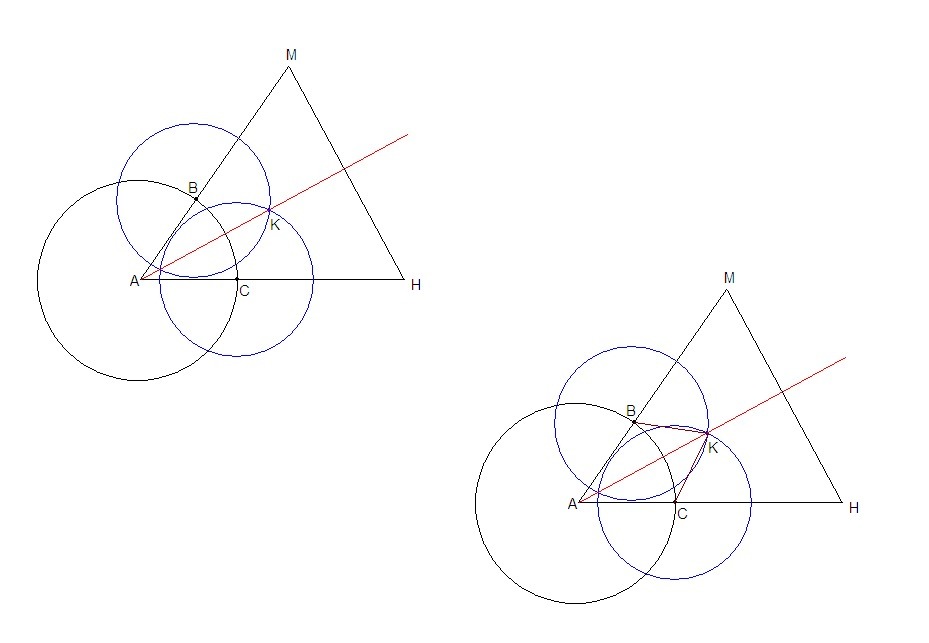
1. Проведем окружность произвольного радиуса (R) с центром в вершине угла А.
Точки пересечения окружности со сторонами угла - В и С.
2. Проведем две окружности одинакового произвольного радиуса (r) с центрами в точках В и С.
К - точка пересечения этих окружностей внутри угла.
3. Проводим луч АК.
АК - искомая биссектриса.

Доказательство:
АВ = АС = R как радиусы первой окружности,
ВК = СК = r как равные радиусы вторых окружностей,
АК - общая сторона для треугольников АВК и АСК, ⇒
ΔАВК = ΔАСК по трем сторонам.

В равных треугольниках напротив равных сторон лежат равные углы, значит
∠ВАК = ∠САК, следовательно
АК - биссектриса угла А.