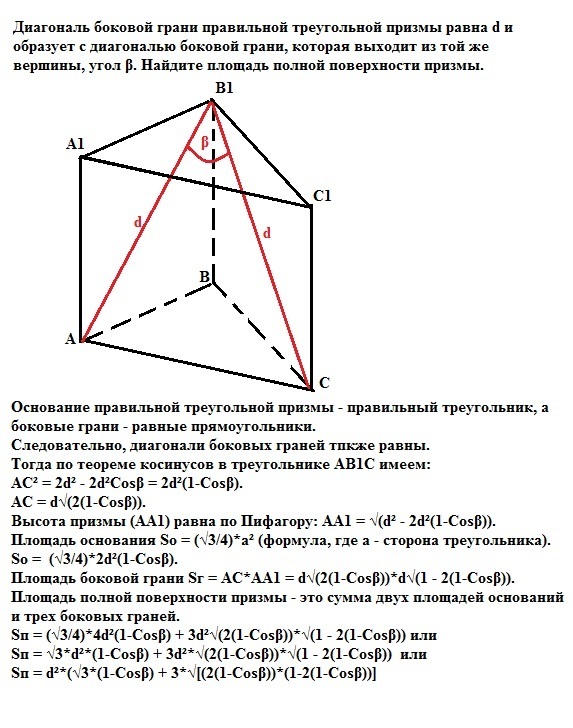
Диагональ боковой грани правильной треугольной призмы равна d и образует с диагональю боковой грани, которая выходит из той же вершины, угол β. Найдите площадь полной поверхности призмы.

Основание правильной треугольной призмы - правильный треугольник, а боковые грани - равные прямоугольники.
Следовательно, диагонали боковых граней также равны.
Тогда по теореме косинусов в треугольнике АВ1С имеем:
АС² = 2d² - 2d²Cosβ = 2d²(1-Cosβ).
АС = d√(2(1-Cosβ)).
Высота призмы (АА1) равна по Пифагору: АА1 = √(d² - 2d²(1-Cosβ)).
Площадь основания So = (√3/4)*a² (формула, где а - сторона треугольника).
So = (√3/4)*2d²(1-Cosβ).
Площадь боковой грани Sг = AC*AA1 = d√(2(1-Cosβ))*d√(1 - 2(1-Cosβ)).
Площадь полной поверхности призмы - это сумма двух площадей оснований и трех боковых граней.
Sп = (√3/4)*4d²(1-Cosβ) + 3d²√(2(1-Cosβ))*√(1 - 2(1-Cosβ)) или
Sп = √3*d²*(1-Cosβ) + 3d²*√(2(1-Cosβ))*√(1 - 2(1-Cosβ)) или
Sп = d²*(√3*(1-Cosβ) + 3*√[(2(1-Cosβ))*(1-2(1-Cosβ))]