Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 06:22
1081
Указать какому промежутку принадлежит сумма корней уравнения: 7x^2-3-15=0
2
ответа
Как полагаю я, перед моими глазами не уравнение вида  , а квадратное. Посоветовал бы для начала умножить все части уравнения на –1, получив при этом уравнение вида
, а квадратное. Посоветовал бы для начала умножить все части уравнения на –1, получив при этом уравнение вида  , уже легче поддающееся решению.
, уже легче поддающееся решению.
 , или равен
, или равен  , что в калькуляторе равно примерно 20,712...
, что в калькуляторе равно примерно 20,712...
Дискриминант мы сосчитали – равен он квадратному корню из четыреста двадцати девяти, а вот корни уравнения мы ещё не сосчитали. Займёмся этим.

Счесть корни фактически невозможно, печаль. Сумма корней уравнения (а иначе ) расписывается следующим образом (конкретно для данного уравнения):
) расписывается следующим образом (конкретно для данного уравнения):
 и равна она, вообщем-то, шести четырнадцатым – обозначим её переменной α. Теперь же начертим числовую прямую, обозначив на ней α.
и равна она, вообщем-то, шести четырнадцатым – обозначим её переменной α. Теперь же начертим числовую прямую, обозначив на ней α.
\\\\\\\\0/////α///
––––––|–––––––>
где , или равно
, или равно  .
.
Тогда промежуток, принадлежащий этому значения, имеет следующий вид:
x∈(–∞; α)∪(α; +∞), ну либо x∈(–∞; )∪(
)∪( ; +∞)
; +∞)
Дискриминант мы сосчитали – равен он квадратному корню из четыреста двадцати девяти, а вот корни уравнения мы ещё не сосчитали. Займёмся этим.
Счесть корни фактически невозможно, печаль. Сумма корней уравнения (а иначе
\\\\\\\\0/////α///
––––––|–––––––>
где
Тогда промежуток, принадлежащий этому значения, имеет следующий вид:
x∈(–∞; α)∪(α; +∞), ну либо x∈(–∞;
0
·
Хороший ответ
4 апреля 2023 06:22
Там где 3 ты потерял х, только в том случае мы получаем дискриминант. У меня не получается извлечь корень, он не извлекается. А вот промежутки я написал и на числовой прямой указал.
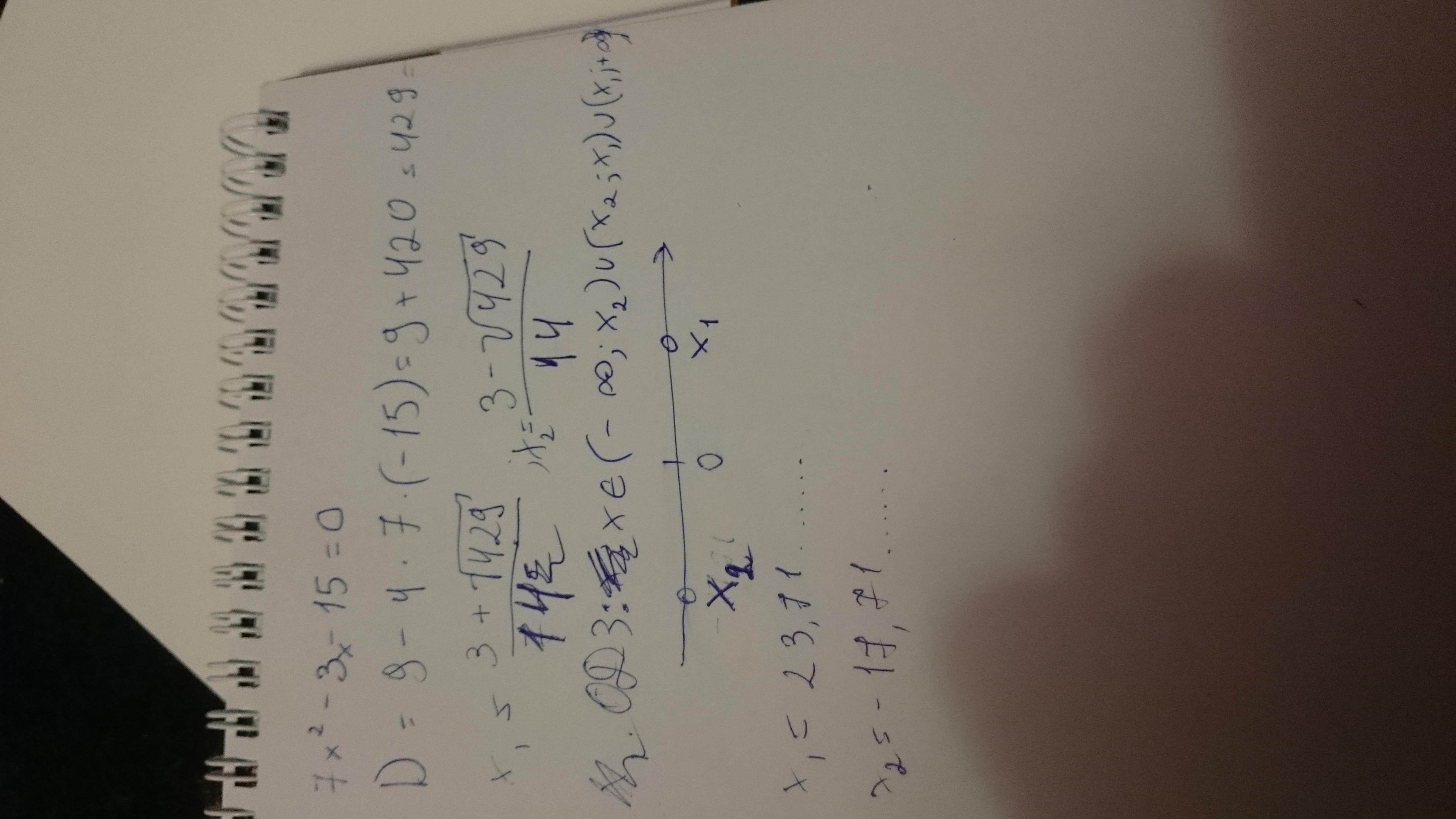
0
4 апреля 2023 06:22
Остались вопросы?
Еще вопросы по категории Математика
Через сколько секунд закончится 10 минут?...
Задача 5 :Из 20 кг кедровых орехов можно получить 5кг масла.Сколько кедровых орехов надо взять,чтобы получилось 20 кг масла. ПОМОГИТЕ РЕШИТЬ ЗАДАЧУ!!...
ариант 3:...
Расставьте числа от 1 до 6 на поле 6 × 6 так, чтобы в каждом столбце и в каждой строке числа не повторялись. Если между двумя соседними по стороне кле...
Чему равно произведение 11 и 12, умноженное на произведение 8 и 9?...