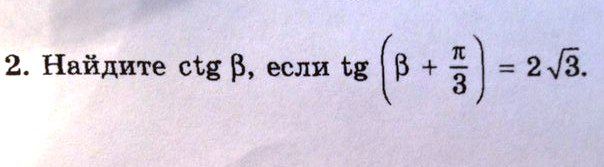Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
Tg(b + pi/3) = 2√3
tg(b + pi/3) = (tgb + tg(pi/3))/(1 - tgb*tg(pi/3)) = (tgb + √3) / (1 - √3*tgb) = 2√3
ctgb = 1/tgb
(tgb + √3) / (1 - √3*tgb) = 2√3
2√3*(1 - √3*tgb) = tgb + √3
2√3 - 6tgb = tgb + √3
7tgb = √3
tgb = √3/7
ctgb = 7/√3
tg(b + pi/3) = (tgb + tg(pi/3))/(1 - tgb*tg(pi/3)) = (tgb + √3) / (1 - √3*tgb) = 2√3
ctgb = 1/tgb
(tgb + √3) / (1 - √3*tgb) = 2√3
2√3*(1 - √3*tgb) = tgb + √3
2√3 - 6tgb = tgb + √3
7tgb = √3
tgb = √3/7
ctgb = 7/√3
0
·
Хороший ответ
4 апреля 2023 07:15
Остались вопросы?
Еще вопросы по категории Алгебра
Помогите решить! Очень нужно! Выписаны первые несколько членов геометрической прогрессии. 125; -100; 80; ... Найдите ее пятый член. ______ И с об...
Конкурс исполнителей проводится в 4 дня. Всего заявлено 80 выступлений- по одному от каждой страны. В первый день 14 выступлений,остальные распределен...
Чему равна эта сторона? Учи.ру, помогите плиз....
Каждый час между двумя соседними кустами крапивы в ряду вырастает еще два таких же. Сколько кустов нужно посадить изначально, чтобы через три часа общ...
тригонометрия...