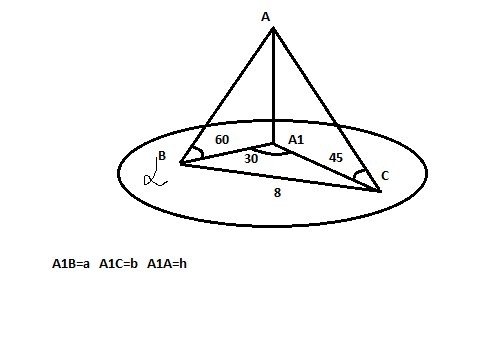
СРОЧНО, ПОМОГИТЕ ПЖИз некоторой точки проведены к плоскости две наклонные, образующие с ней углы 45° и 60°. Найдите длину меньшей наклонной, если расстояние между основаниями наклонных равно 8, а угол между их проекциями на плоскость равен 30°.
Нужно решение и ответ.

АВ^2=8^2=64=a^2+b^2-2abcos30=a^2+b^2-ab√3
(по т. косинусов)
мне нужно еще одно уравнение, связывающее а и b,
мне поможет высота h
Из ΔАВА1 tg 60=h/a=√3; h=a√3
из ΔАА1С tg45=h/b=1; h=b; a√3=b
подставлю в верхнее уравнение
a^2+(a√3)^2-a*a√3*√3=64
a^2+3a^2-3a^2=64
a=8
Чтобы найди длину меньшей наклонной АВ=a/cos60=8/(1/2)=16