Радиус описанной около равностороннего треугольника окружности равен 8см. Найдите периметр этого треугольника и радиус вписанной окружности. ВСЁ ПОДРОБНО т.к. на контрошу (желательно с рисунком)

1 ответ

Посмотреть ответы

DevAdmin

1690

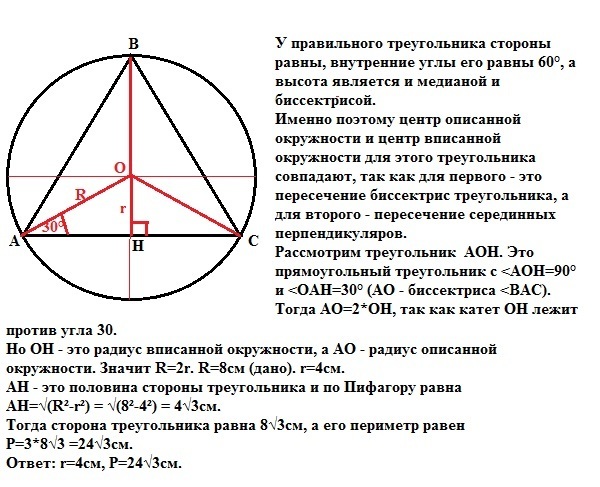
У правильного треугольника стороны равны, внутренние углы его равны 60°, а высота является и медианой и биссектрисой.
Именно поэтому центр описанной окружности и центр вписанной окружности для этого треугольника совпадают, так как для первого - это пересечение биссектрис треугольника, а для второго - пересечение серединных перпендикуляров.
Рассмотрим треугольник АОН. Это прямоугольный треугольник с <АOH=90° и <OAH=30° (АО - биссектриса <ВАС).
Тогда АО=2*ОН, так как катет ОН лежит против угла 30°.
Но ОН - это радиус вписанной окружности, а АО - радиус описанной окружности. Значит R=2r. R=8см (дано). r=4см.
АН - это половина стороны треугольника и по Пифагору равна
АН=√(R²-r²) = √(8²-4²) = 4√3см.
Тогда сторона треугольника равна 8√3см, а его периметр равен
Р=3*8√3 =24√3см.
Ответ: r=4см, Р=24√3см.

Хороший ответ

4 апреля 2023 09:58

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Билет 6 1. Определение параллельных прямых. Признаки параллельности прямых (доказательство одного из признаков по выбору учащегося). 2. Определение т... В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстоя... Прямая, параллельная основаниям MP и NK трапеции MNKP, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и K... Через вершину квадрата ABCD проведена прямая ВМ, перпендикулярная его плоскости. Докажите, что: 1) прямая AD перпендикулярна плоскости прямых АВ и ВМ;... диагональ прямоугольника ABCD пересекается в точке О, LABO = 37°. Найдите угол AOD....