Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 15:47
2996
Построить график функции f(x)=x³-x²-x+² на отрезке [-1;2]
1
ответ
Проведем небольшое исследование функции f(x) = x³ - x² - x + 2, с учетом того, что x ∈ [-1; 2]
Найдем её производную:
f'(x) = 3x² - 2x² - 1
Найдем нули производной:
f'(x) = 0
3x² - 2x² - 1 = 0
D = 4 + 12 = 16
x = (2 ± 4) / 6
x₁ = -1/3 ∈ [-1; 2]; x₂ = 1 ∈ [-1; 2]
При x ∈ [-1; -1/3] f'(x) ≥ 0, f(x) - возрастает
x = -1/3 - точка максимума; f(-1/3) = 43/27 ≈ 2,2
При x ∈ [-1/3; 1] f'(x) ≤ 0, f(x) - убывает
x = 1 - точка минимума; f(1) = 1
При x ∈ [1; 2] f'(x) ≥ 0, f(x) - возрастает
Значения f(x) в концах отрезка [-1; 2]:
f(-1) = 1; f(2) = 4
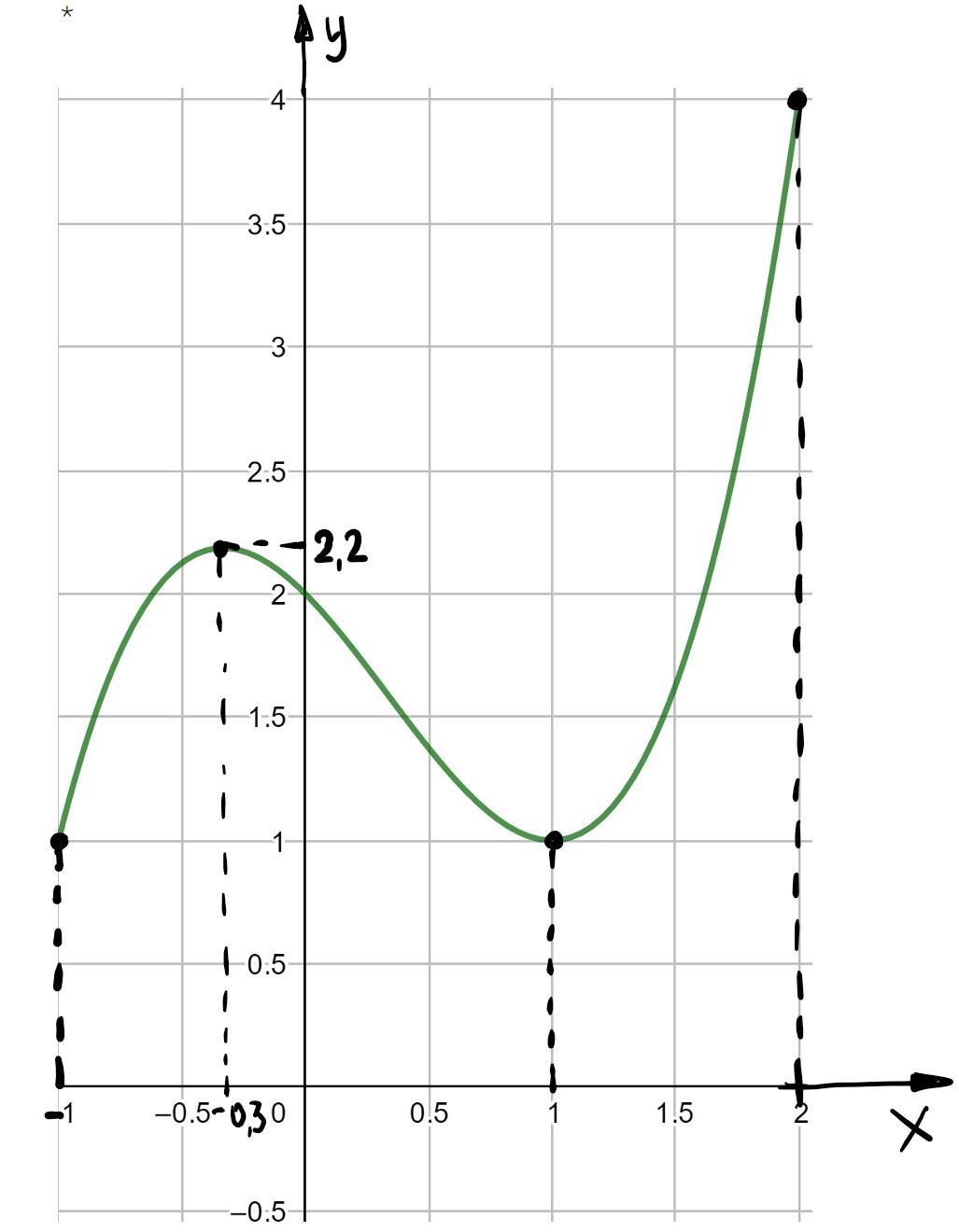
Точки для построения графика: A(-0,3; 2,2) - локальный максимум, B(1, 1) - локальный минимум, С(-1; 1), D(2; 4)
Найдем её производную:
f'(x) = 3x² - 2x² - 1
Найдем нули производной:
f'(x) = 0
3x² - 2x² - 1 = 0
D = 4 + 12 = 16
x = (2 ± 4) / 6
x₁ = -1/3 ∈ [-1; 2]; x₂ = 1 ∈ [-1; 2]
При x ∈ [-1; -1/3] f'(x) ≥ 0, f(x) - возрастает
x = -1/3 - точка максимума; f(-1/3) = 43/27 ≈ 2,2
При x ∈ [-1/3; 1] f'(x) ≤ 0, f(x) - убывает
x = 1 - точка минимума; f(1) = 1
При x ∈ [1; 2] f'(x) ≥ 0, f(x) - возрастает
Значения f(x) в концах отрезка [-1; 2]:
f(-1) = 1; f(2) = 4
Точки для построения графика: A(-0,3; 2,2) - локальный максимум, B(1, 1) - локальный минимум, С(-1; 1), D(2; 4)
0
·
Хороший ответ
4 апреля 2023 15:47
Остались вопросы?
Еще вопросы по категории Математика
Какой денежный эквивалент имеет число 1000000?...
Дана развертка прямоугольного параллелепипеда. Найди измерения прямоугольного параллелепипеда (a, b, c) и сумму площадей всех граней. a (длина) = см;...
Найдите площадь четырехугольника, изображенного на рисунке: а=10см б=8см с=3см...
Какие действия можно выражать с помощью презент континиус?...
определи какие вычисления можно выполнить устно а какие письмино найди значение выражений проверь себя с помощью калькулятора...