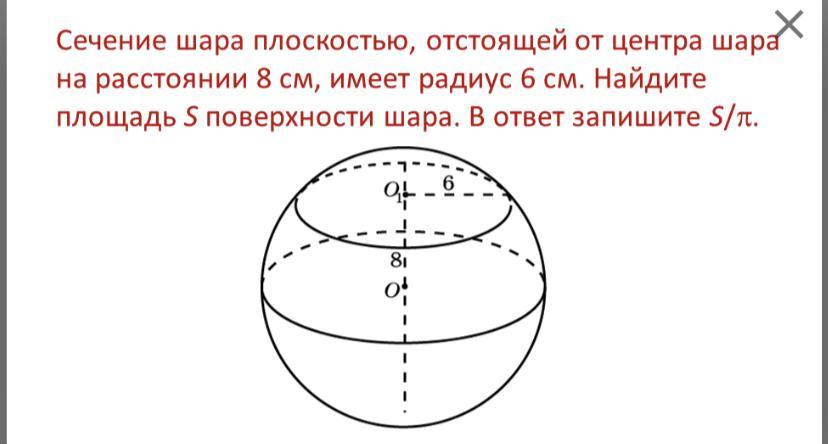
Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите площадь поверхности шара.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ: 1256 см²

Пошаговое объяснение:
При сечении шара плоскостью имеем прямоугольный треугольник, где расстояние сечения от центра шара и его радиус являются катетами Согласно т. Пифагора гипотенуза его- это радиус шара и равна r=√(8²+6²)=√64+36=√100 = 10см , отсюда
Площадь поверхности шара равна:
S=4πr²=4π*10²=400π=400*3,14=1256 см²

Хороший ответ

4 апреля 2023 15:47

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Какие инструкции нужно выполнить для задания '1 мом в ком'?... Из вершины развернутого угла проведен луч так, что он делит развернутый угол на 2 угла ,один из которых меньше второго на 50 градусов. Найдите величин... Какие есть примеры слов с непроизносимыми согласными в русском языке?... Реши удобным способом 45+38+5+2... 1) В часах: 2 суток,10 суток,12 часов,120 минут. 2)в сутках: 48 часов,72 часов,96 часов,2 недели 3)в месяцах: 2 года,8 лет и 4 месяца 4)в гадах: 24 ме...