Найдите площадь фигуры,ограниченной линиями: y=5x-x^2 и y=x+3

1 ответ

Посмотреть ответы

Megamozg

2205

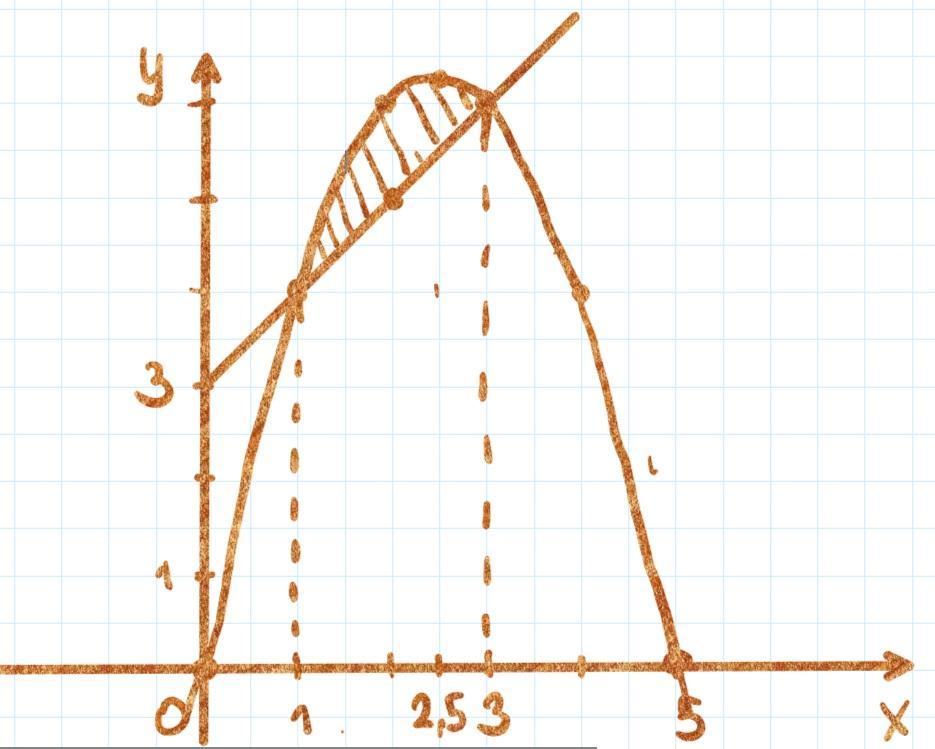
1) Строим графики функций (см. рисунок):
y = 5x - x² = f(x) - квадратичная, график - парабола (ветви - вниз)
Нули (y = 0): 5x - x² = 0; x·(5 - x) = 0;
x = 0 или x = 5
Вершина: x₀ = 5/2 = 2,5; y₀ = 2,5² = 6,25
y = x + 3 = g(x) - линейная, график - прямая
Точки для построения: (0; 3); (2; 5)
2) Находим абсциссы точек пересечения графиков:
5x - x² = x + 3
x² - 4x + 3 = 0
D = 16 - 12 = 4
x = (4 ± 2) / 2
x₁ = 3; x₂ = 1
3) Площадь "между графиками" находим по формуле:
$S=\int\limits^a_b {(f(x)-g(x))} \, dx$
В нашем случае a = 1; b = 3
$S=\int\limits^3_1 {(5x-x^2-x-3)} \, dx =\int\limits^3_1 {(-x^2+4x-3)} \, dx =-\dfrac+2x^2-3x\left\ \begin{|}3\\1\end =$ $=-9+18-9+\frac-2+3=1 \frac 1 3$

Хороший ответ

4 апреля 2023 16:11

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Упростите выражение и найдите его значение при . В ответе запишите полученное число.... Сколько чётных четырёхзначных чисел можно составить из цифр 6, 7, 8, 9 (без их повторения).... Найдите кв корни по дискриминату. Номеи 244 пожалуйста срочно сейчас... Известно, что 3<х<8, 2<у<6, Оцените значение выражение 1.2х+у 2.ху. 3.х-у пж только решите правильно... Пожалуйста помогите решить задачи 1. В футбольной секции первоначально занималось в 3 раза больше учеников, чем в баскетбольной. Когда в футбольную се...