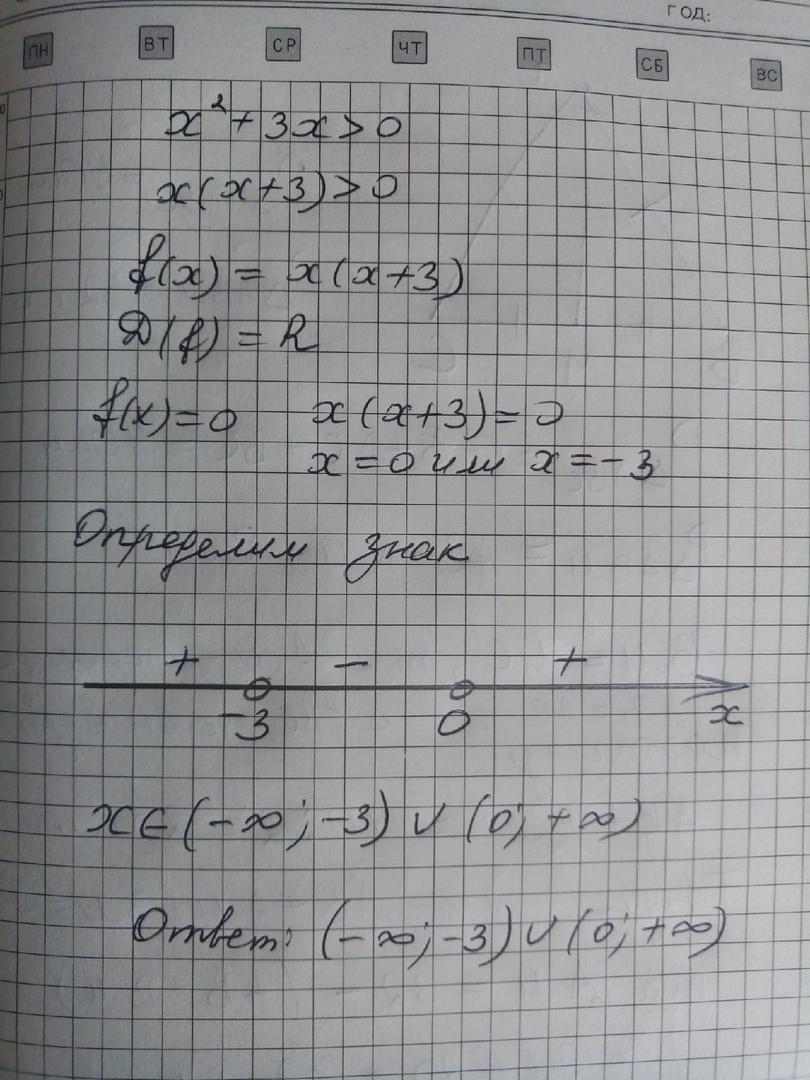Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
Ответ:
(-∞; -3)∪(0; +∞)
Объяснение:
Дано неравенство
x²+3·x>0
Рассмотрим функцию: f(x)=x²+3·x. Чтобы применит метод интервалов определим нули функции f(x):
f(x)=0 ⇔ x²+3·x=0 ⇔ (x+3)·x=0 ⇔ x₁= -3, x₂=0.
Нули функции f(x) делят ось Ох на промежутки (-∞; -3), (-3; 0) и (0; +∞), в каждом из которых функция f(x) сохраняет свой знак. Поэтому:
1) при x∈(-∞; -3) функция f(x)=x²+3·x>0, так как, например при -5∈(-∞; -3):
f(-5)=(-5)²+3·(-5)=25-15=10>0;
2) при x∈(-3; 0) функция f(x)=x²+3·x<0, так как, например при -2∈(-3; 0):
f(-2)=(-2)²+3·(-2)=4-6=-2<0;
3) при x∈(0; +∞) функция f(x)=x²+3·x>0, так как, например при 1∈(0; +∞):
f(1)=1²+3·1=1+3=4>0.
Тогда решением неравенства x²+3·x>0 будет:
x∈(-∞; -3)∪(0; +∞).
(-∞; -3)∪(0; +∞)
Объяснение:
Дано неравенство
x²+3·x>0
Рассмотрим функцию: f(x)=x²+3·x. Чтобы применит метод интервалов определим нули функции f(x):
f(x)=0 ⇔ x²+3·x=0 ⇔ (x+3)·x=0 ⇔ x₁= -3, x₂=0.
Нули функции f(x) делят ось Ох на промежутки (-∞; -3), (-3; 0) и (0; +∞), в каждом из которых функция f(x) сохраняет свой знак. Поэтому:
1) при x∈(-∞; -3) функция f(x)=x²+3·x>0, так как, например при -5∈(-∞; -3):
f(-5)=(-5)²+3·(-5)=25-15=10>0;
2) при x∈(-3; 0) функция f(x)=x²+3·x<0, так как, например при -2∈(-3; 0):
f(-2)=(-2)²+3·(-2)=4-6=-2<0;
3) при x∈(0; +∞) функция f(x)=x²+3·x>0, так как, например при 1∈(0; +∞):
f(1)=1²+3·1=1+3=4>0.
Тогда решением неравенства x²+3·x>0 будет:
x∈(-∞; -3)∪(0; +∞).
0
·
Хороший ответ
4 апреля 2023 20:12
Остались вопросы?
Еще вопросы по категории Алгебра
Разложите на множители : 1) 100-a² 2) x²+10x+25 3) 36y²-49 4) 16a²-24ab+9b2...
Построить график функции y=2x-4 , укажите при каком значении y, значение x=1,5...
Исследовать функцию y=x-4x2(квадрат)...
Не виконуючи побудови, знайти координати точки перетину графіків функцій: Не выполняя постоения, найдите координаты точки пересечения графиков функций...
Существует ли треугольник со сторонами: а) 1 м, 2м и 3 м; б) 1,2 дм, 1 дм и 2,4 дм? пожалуйста, поподробнее ок?...