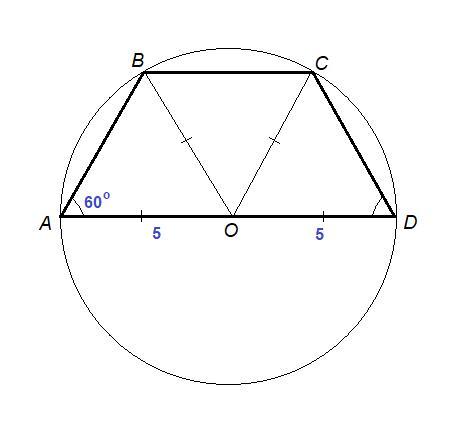
Трапеция вписана в окружность радиуса 5, причём один из её углов равен 60°. Найдите периметр трапеции, если одно её основание является диаметром окружности.(Помогите пожалуйста подробно)

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
Периметр трапеции: 25
Объяснение:

Если трапеция вписана в окружность, то она равнобедренная.

ОА = ОВ = ОС = OD = 5 как радиусы.
Треугольник АОВ равнобедренный, значит ∠ОВА = ∠ОАВ = 60°, но тогда
∠АОВ = 180° - (60° + 60°) = 180° - 120° = 60°, то есть
ΔАОВ равносторонний,
АВ = АО = 5

Вообще, если в равнобедренном треугольнике любой угол равен 60°, то этот треугольник равносторонний.

CD = AB = 5, так как трапеция равнобедренная.
ΔCOD так же равносторонний, значит ∠COD = 60°.
Углы АОВ, ВОС и COD составляют в сумме развернутый угол, тогда
∠ВОС = 180° - (∠АОВ + ∠COD) = 180° - (60° + 60°) = 180° - 120° = 60°
Значит, ΔВОС тоже равносторонний,
ВС = ОВ = 5
Периметр трапеции:
P = AB + BC + CD + AD = 5 + 5 + 5 + 10 = 25

Хороший ответ

5 апреля 2023 01:42

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике ABC A(-3;4), B(2;8), C(2;-1). Найди среднюю линию KP треугольника ABC, где точки K и P&nbs... Дан треугольник АВС. Плоскость, пересекая стороны АС и ВС треугольника АВС соответственно в точках А 1 и В 1 , делит их в отношении АА 1 :А 1 С= ВВ... Диагональ боковой грани правильной треугольной призмы наклонена к плоскости основания под углом альфа, а площадь этой грани равна Q. Найдите площадь п... Какие прямые называются параллельными ???... В треугольнике CDE точка K лежит на отрезки CE,причем угол CKD-острый угол.Докажите,что DE>Dk Помогите пж срочно надо Решите с доказательством реш...