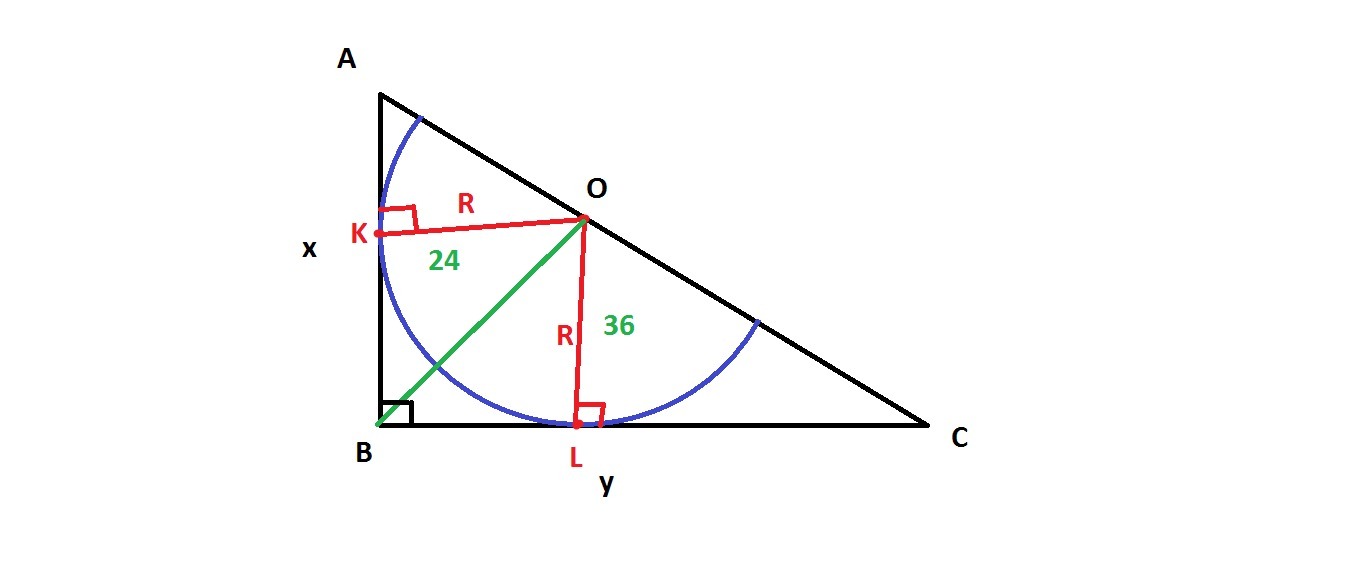
Полуокружность,центр O которого лежит на гипотенузе AC прямоугольного треугольника ABC, касается катетов. Найдите площадь квадрата со стороной AC, если отрезок BO разбивает площадь треугольника на части 24 см^2 и 36 см^2.

2 ответа

Посмотреть ответы

Megamozg

2205

Площадь ΔАВС=24+36=60

Пусть АВ=х, а ВС=у
Проведем радиусы в точки касания К и L, то есть ОК=OL=R
По теореме радиус, проведенный в точку касания, перпендикулярен самой касательной. То есть ∠АКО=∠ВLO=90°

$S_= \fracah= \frac *BC*OL=\frac*y*R \\ \\ S_=\frac*AB*OK=\frac*x*R$

по условию площадь ΔАОВ=24 и площадь ΔВОС=36.

$\left \{ {{ \frac*y*R=36} \atop {\frac*x*R=24}} \right. \ \ =\ \textgreater \ \ \ \left \{ { \atop } \right.$

поделим первое уравнение на второе:

$\frac= \frac \ \ =\ \textgreater \ \ \ \frac =1.5$

$S_= \frac *AB*BC=\frac *x*y$

зная, что площадь ΔАВС=60, запишем еще одну систему:

$\left \{ {{\frac *x*y=60} \atop {\frac =1.5}} \right. \ \ =\ \textgreater \ \ \ \left \{ { \atop y=1.5x}} \right. \\ \\ x*1.5x=120 \\ \\ 1.5x^2=120 \\ \\ x^2=120/1.5=80 \\ \\ x=4 \sqrt \\ \\ y=1.5x=1.5*4 \sqrt =6 \sqrt$

Площадь квадрата со стороной АС = АС²

АС² найдем по теореме Пифагора из ΔАВС:

$AC^2=AB^2+BC^2=x^2+y^2=(4 \sqrt )^2+(6 \sqrt )^2=80+180=260 \\ \\$

ОТВЕТ: 260 см²

Хороший ответ

5 апреля 2023 02:28

DevAdmin

1720

Радиус окружности перпендикулярен касательной к ней.

Значит высоты обоих треугольников будут равны.

AB*r/2=24
BC*r/2=36

Приравняем r/2.

r/2=24/AB=36/BC

BC=1.5AB

Площадь прямоугольного треугольника равна произведению катетов делённому на 2, следовательно:

24+36=BC*AB/2
60=1.5AB^2/2
120=1.5AB^2
AB^2=80

BC^2=2.25AB^2
BC^2=180

По т. Пифагора:

AC^2=AB^2+BC^2=80+180=260

Площадь квадрата равна его стороне в квадрате, то есть:

S=AC^2=260

Ответ: 260.

5 апреля 2023 02:28

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Точка О принадлежит отрезку CD, CO =16 см отрезок OD на 9 см меньше отрезка CO НАЙДИТЕ ДЛИНУ ОТРЕЗКА CD Помогите... На карте с масштабом 1 : 10000 расстояние между двумя пунктами равно 12 см.Найти расстояние между пунктами на местности. Закончите решение задачи. Пус... Какой остаток от деления 10 на 12?... Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба... Путешественник 3 ч ехал на автобусе и 3 ч-на поезде, преодолев за это время путь в 390 км. Найдите скорость автобуса, если она втрое меньше скорости п...