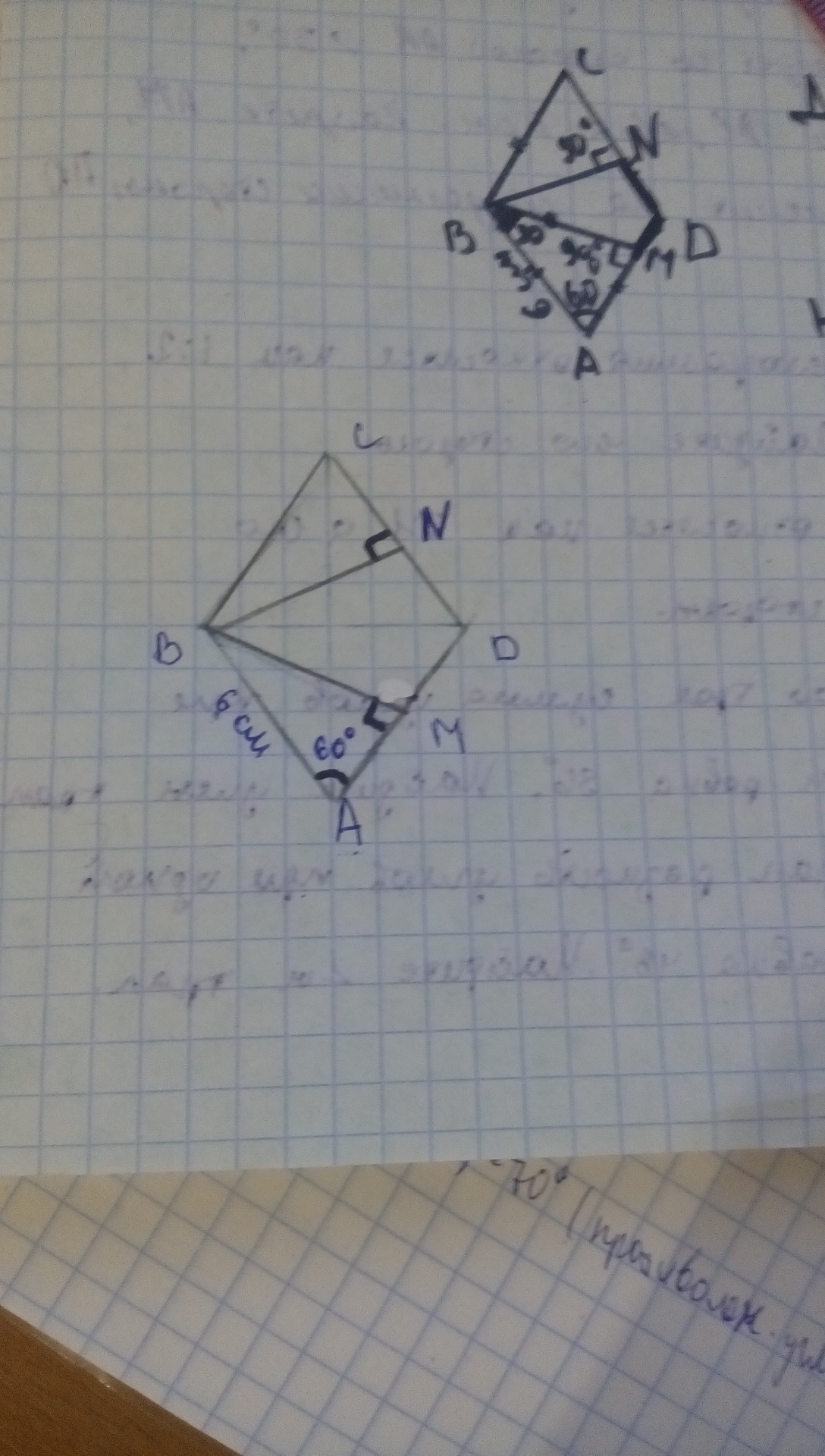
ОЧЕНЬ СРОЧНО!!!!!! ПОМОГИТЕ!В ромбе ABCD угол А равен 60 градусов, сторона АВ=6 см. Из вершины В на тороны АD и СD проведены перпендикуляры BM и BN. Чему равна сумма сторон MD+DN

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
MD+DN = 6 см.
Пошаговое объяснение:
Свойства ромба: в ромбе все стороны равны; в ромбе противолежащие углы равны.
1) Рассмотрим ΔABM.
BM ⊥ AD, ∠AMB = 90° по условию.
∠BAM = 60° по условию. ⇒ ∠ABM = 30°.
В прямоугольном треугольнике катет, лежащий против угла 30° равен половине гипотенузы. AM = BA / 2 = 6 см / 2 = 3 см.
2) AD = 6 см. Отрезок MD = AD - AM = 6 см - 3 см = 3 см.
3) Аналогично в ΔBCN.
BN ⊥ CD, ∠BNC = 90° по условию.
∠BCN = 60° ⇒ ∠CBN = 30°.
В прямоугольном треугольнике катет, лежащий против угла 30° равен половине гипотенузы. CN = CB / 2 = 6 см / 2 = 3 см.
Отрезок ND = CD - CN = 6 см - 3 см = 3 см.
4) Cумма отрезков MD + DN = 3 см + 3 см = 6 см.

Хороший ответ

5 апреля 2023 03:10

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Какое количество времени обозначает число 10?... 3/8 доли это как? Вот я понимаю, что такое 1/4 доля, это когда один торт , а его порезали на 4 части. А вот 3/8 доли? это как? Объясните пожалуйста=-... Что значит выражение '1 3 в пятой степени'?... Первый садовый насос перекачивает 9 литров воды за 1 минуту, второй насос перекачивает тот же объём воды за 2 минуты. Сколько минут эти два насоса дол... Сколько единиц составляет задание '10 ед'?...