Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60°. Найдите объём пирамиды.

1 ответ

Посмотреть ответы

Megamozg

2205

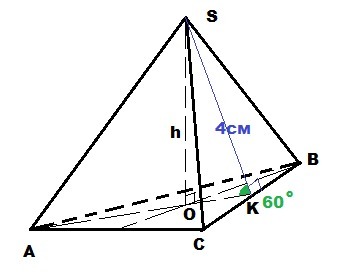
Правильная треугольная пирамида SABC
Двугранный угол ∠AKS = 60°
Апофема SK = 4 см

Высота SO правильной пирамиды опускается в центр окружности, вписанной в равносторонний ΔABC ⇒ r = ОК
ΔSOK прямоугольный : ∠SOK = 90°
r = OK = SK*cos 60° = 4*1/2 = 2 см
h = SO = SK*sin 60° = 4*√3/2 = 2√3 см
Если в равносторонний ΔABC вписана окружность с радиусом r=2 см, то сторона треугольника
a = CB = 2√3 r = 2√3 * 2 = 4√3 см
Площадь равностороннего треугольника
S = a²√3/4 = (4√3)²*√3/4 = 48*√3/4 = 12√3 см²

Объем пирамиды
V = 1/3 S h = 1/3*12√3 *2√3 = 24 см³

Хороший ответ

1 сентября 2022 20:49

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Дана четырёхугольная пирамида,в основании которой лежит ромб.Все высоты боковых граней,проведённые из вершин,равны 53.Высота пирамиды равна 45.Острый... Большая боковая сторона прямоугольной трапеции равна 12√2 см, а острый угол - 45°, найдите площадь трапеции, если известно, что в трапецию можно вписа... Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60 градусов, если плоскость... Помоогите срочно Биссектриса равностороннего треугольника равна половине стороны треугольника.Это утверждение... 1.может быть верно 2.верно всегда 3.н... Нужно решить вместе с чертежом) Два внешних ушла треугольника равны 142 градуса и 82 градуса. Найдите углы, на которые высота треугольника делит его н...