Дана полуокружность. Найдите геометрическое место середин отрезков, концы которых лежат на этой полуокружности

1 ответ

Посмотреть ответы

Megamozg

2200

Ответ:
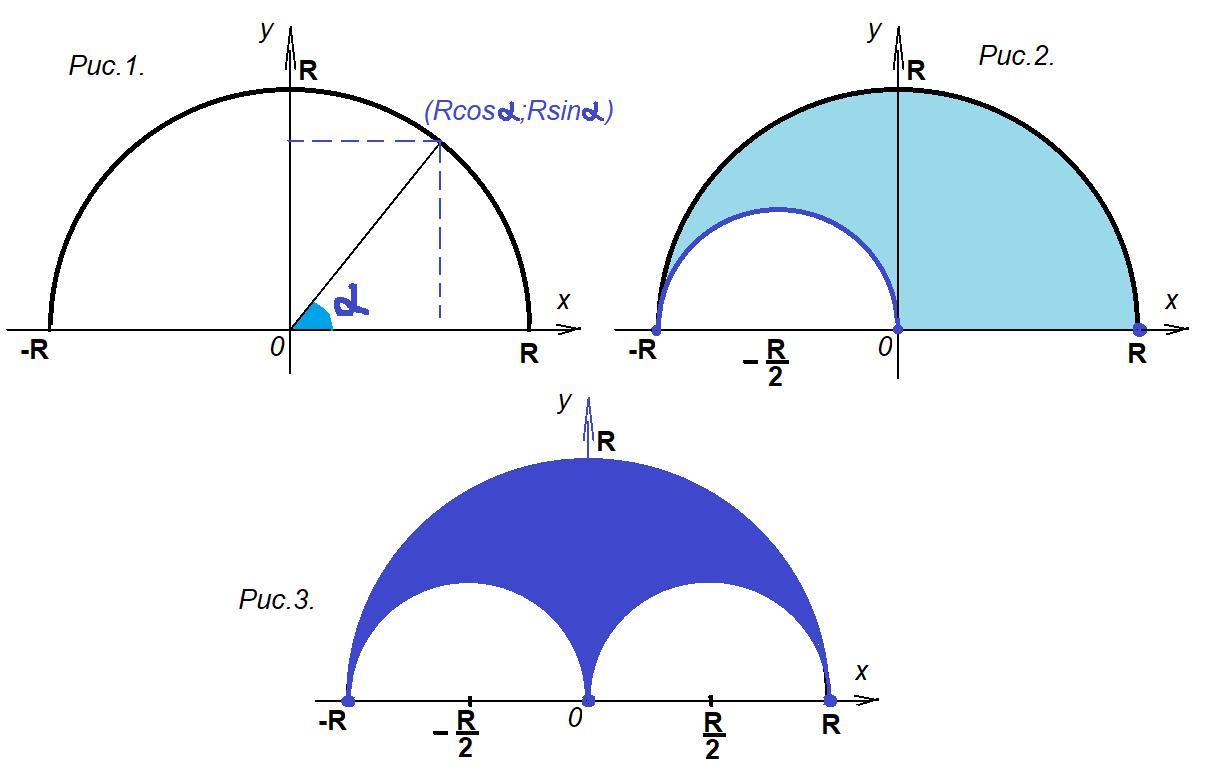
Геометрическое место середин отрезков, концы которых лежат на полуокружности, представлено в приложении на рис. 3.
Пошаговое объяснение:
Пусть дана полуокружность с радиусом R и центром в точке $(0;0)$ (рис. 1.).
Любую точку этой полуокружности можно представить в виде:
$\displaystyle\left \{ { \atop } \right. ;\ \ \ \ 0^\circ\le \alpha \le 180^\circ;\ \ \ \ \left \ {{-R\le x\le R} \atop {\ \ \ 0\le y \le R}} \right.$
Максимальная длина отрезка, концы которого лежат на полуокружности, равна диаметру. Середина такого отрезка - это центр полуокружности. Геометрическое место середины отрезка-диаметра в системе координат - это точка $(0;0).$
Минимальная длина отрезка, концы которого лежат на полуокружности, равна нулю, если концы отрезка совпадают. В этом случае середина отрезка совпадает с концами отрезка. Геометрическое место середин вырожденных отрезков - сама полуокружность.
Середины произвольных отрезков будут находиться в пределах полукруга, ограниченного заданной полуокружностью и осью Ох.
Координаты середины любого отрезка можно посчитать как среднее арифметическое координат концов отрезка:
$x_c=\dfrac2;\ \ \ \ y_c=\dfrac2$
Возьмём две точки полуокружности $(x_1; y_1);\ (x_2; y_2).$ Одна точка произвольная, а вторая находится в первой четверти.
Для координат любых этих точек выполняются условия:
$x_1\ge -R;\ \ \ y_1\ge 0;\\x_2=R\cos\alpha\ge0;\ \ \ y_2=R\sin\alpha\ge 0;\\0^\circ\le\alpha \le 90^\circ$
Тогда для координат середины такого отрезка выполняются неравенства:
$\displaystyle\left \{ {2\ge\dfrac{-R+R\cos\alpha }2} \atop 2}\ge\dfrac2} \right.$
Преобразуем неравенства:
$\displaystyle\left \{ {2} \atop 2\ \ \ \ \ } \right.\ \ \ \Leftrightarrow\ \ \ \left \{ { \right.$
В обоих неравенствах правые части неотрицательные, левые не меньше их, то есть тоже неотрицательные. Возведём в квадрат и сложим оба неравенства:
$\displaystyle\left \{ {{\left(x_c+\dfrac R2\right)^2\ge\left(\dfrac R2\right)^2\cdot \cos^2\alpha \atop \right.+\\-----------------\\\left(x_c+\dfrac R2\right)^2+y_c^2\ge\left(\dfrac R2\right)^2\cdot \cos^2\alpha+\left(\dfrac R2\right)^2\cdot \sin^2\alpha\\\\\left(x_c+\dfrac R2\right)^2+y_c^2\ge\left(\dfrac R2\right)^2\cdot \underbrace{\left(\cos^2\alpha+\sin^2\alpha\right)}_{=1}\\\\$

$\left(x_c+\dfrac R2\right)^2+y_c^2=\left(\dfrac R2\right)^2$
Это уравнение окружности с радиусом $\dfrac R2$ и центром в точке $\left(-\dfrac R2;0\right).$
Тогда точки, удовлетворяющие неравенству:
$\left(x_c+\dfrac R2\right)^2+y_c^2\ge\left(\dfrac R2\right)^2$ , лежат либо на окружности, либо вне круга с радиусом $\dfrac R2$ и центром в точке $\left(-\dfrac R2;0\right).$ Рис. 2.

Так как полуокружность симметрична относительно оси Оу, то в первой четверти можно вырезать точно такую же область, в которую середины отрезков попасть не могут. Эта ситуация соответствует условию, что один конец отрезка находится во второй четверти, а второй конец выбран произвольно. Таким образом, все возможные случаи расположения концов отрезков учтены.

На рис.3 синим цветом показано геометрическое место середин отрезков, концы которых лежат на полуокружности.

Хороший ответ

5 апреля 2023 04:35

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Петя купил продукты в чеке указано наименование каждого товара количество и цена например Петя купил две бутылки молока по 60 руб. и заплатил за них 1... Сколько будет, если умножить 1000 на 300?... Сколько слов в списке с корнем зор?... Назови 10 существительных мужского рода.... Какое из слов является словом с непроверяемой гласной: cat, dog, bird?...

Дана полуокружность. Найдите геометрическое место середин отрезков, концы которых лежат на этой полуокружности​

Дана полуокружность. Найдите геометрическое место середин отрезков, концы которых лежат на этой полуокружности