Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 04:52
849
Используйте метод вспомогательного аргумента покажите что уравнение.... помогите пожалуйста....
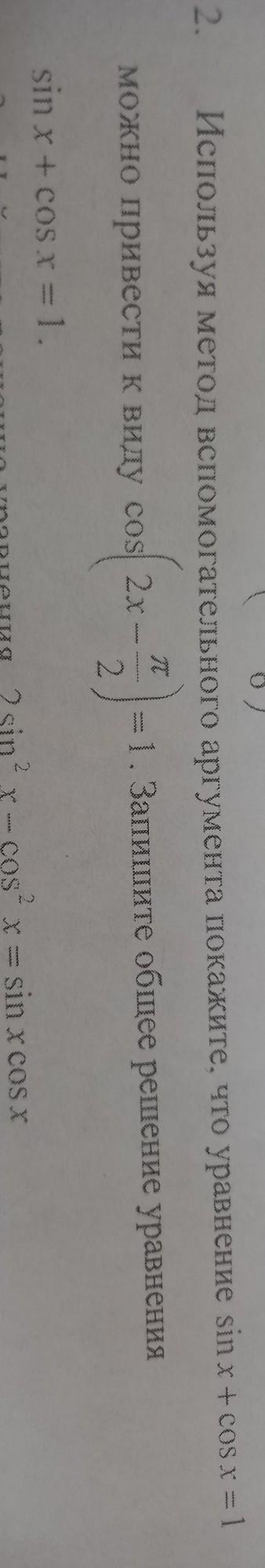
1
ответ
Ответ:





Как видим, нельзя выражение (sinx+cosx) привести к выражению вида сos(2х-П/2) .
Как видим, нельзя выражение (sinx+cosx) привести к выражению вида сos(2х-П/2) .
0
·
Хороший ответ
5 апреля 2023 04:52
Остались вопросы?
Еще вопросы по категории Алгебра
Решить уравнение 1) 27^x = 1/3 2) 400^x = 1/20 3) (1/5)^x = 25 4) (1/3)^x =1/81 5) 3^(x+3)+3^x = 7^(x+1)+5*7^x 6) 2^(x+1)+2^(x-1)-3^(x-1) =3^(x-2)-2^(...
Определите знак выражения cos(-1)sin (-2)...
Преобразуйте в многочлен выражение: (х-2)² - (х-1)(х+2)...
Построить график функции y=arccos(x-1)+1...
а)решите уравнение 4cos^4x - 4cos^2x + 1=0 b) найдите все корни этого уравнения,принадлежащие отрезку[-2П;-П]...