Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 05:40
649
Найдите производную функции1) y= корень 3 степени из 8x
2) y= 1/2 корень 3 степени из x^-2
3) y= 2/x^3
4) y=2/корень из x
5) y= 1/корень 3 степени из x
6) y= 6/ корень 3 степени из x^2
7) y= 1/ корень из 4x^3
8) y= 1/ корень из x^2/3
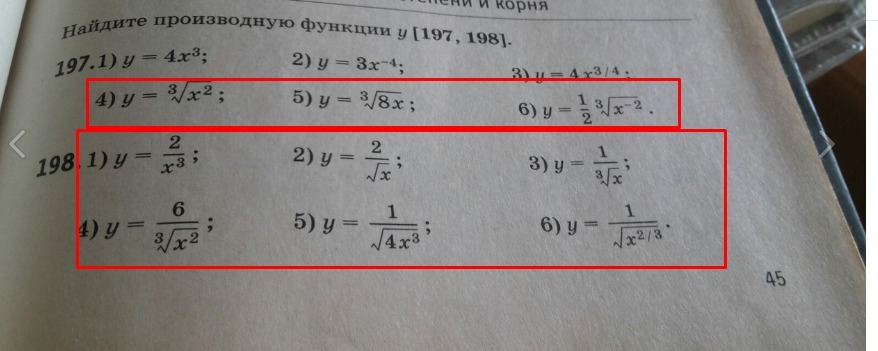
1
ответ
197–ой:
1.
;
2.
;
3.
;
4.![(\sqrt[3])'=(x^{\frac})'=\fracx^{-\frac}](https://tex.z-dn.net/?f=%28%5Csqrt%5B3%5D%7Bx%5E2%7D%29%27%3D%28x%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D%29%27%3D%5Cfrac%7B2%7D%7B3%7Dx%5E%7B-%5Cfrac%7B1%7D%7B3%7D%7D "(\sqrt[3])'=(x^{\frac})'=\fracx^{-\frac}")
;
5.![(\sqrt[3])'=(2\sqrt[3])'=2*(x^{\frac})'=2*\fracx^{-\frac}=\fracx^{-\frac}](https://tex.z-dn.net/?f=%28%5Csqrt%5B3%5D%7B8x%7D%29%27%3D%282%5Csqrt%5B3%5D%7Bx%7D%29%27%3D2%2A%28x%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%29%27%3D2%2A%5Cfrac%7B1%7D%7B3%7Dx%5E%7B-%5Cfrac%7B2%7D%7B3%7D%7D%3D%5Cfrac%7B2%7D%7B3%7Dx%5E%7B-%5Cfrac%7B2%7D%7B3%7D%7D "(\sqrt[3])'=(2\sqrt[3])'=2*(x^{\frac})'=2*\fracx^{-\frac}=\fracx^{-\frac}")
;
6.![(\frac\sqrt[3]})'=\frac*(x^{-\frac})'=\frac*(-\fracx^{-\frac})=-\fracx^{-\frac}](https://tex.z-dn.net/?f=%28%5Cfrac%7B1%7D%7B2%7D%5Csqrt%5B3%5D%7Bx%5E%7B-2%7D%7D%29%27%3D%5Cfrac%7B1%7D%7B2%7D%2A%28x%5E%7B-%5Cfrac%7B2%7D%7B3%7D%7D%29%27%3D%5Cfrac%7B1%7D%7B2%7D%2A%28-%5Cfrac%7B2%7D%7B3%7Dx%5E%7B-%5Cfrac%7B5%7D%7B3%7D%7D%29%3D-%5Cfrac%7B1%7D%7B3%7Dx%5E%7B-%5Cfrac%7B5%7D%7B3%7D%7D "(\frac\sqrt[3]})'=\frac*(x^{-\frac})'=\frac*(-\fracx^{-\frac})=-\fracx^{-\frac}")
.
198–ой:
1.
;
2.
;
3.![(\frac{\sqrt[3]})'=-\frac})'}{(x^{\frac})^2}=-\frac\frac}}}}=-\fracx^{-\frac}](https://tex.z-dn.net/?f=%28%5Cfrac%7B1%7D%7B%5Csqrt%5B3%5D%7Bx%7D%7D%29%27%3D-%5Cfrac%7B1%2A%28x%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%29%27%7D%7B%28x%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%29%5E2%7D%3D-%5Cfrac%7B1%7D%7B3%7D%5Cfrac%7Bx%5E%7B-%5Cfrac%7B2%7D%7B3%7D%7D%7D%7Bx%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D%7D%3D-%5Cfrac%7B1%7D%7B3%7Dx%5E%7B-%5Cfrac%7B4%7D%7B3%7D%7D "(\frac{\sqrt[3]})'=-\frac})'}{(x^{\frac})^2}=-\frac\frac}}}}=-\fracx^{-\frac}")
;
4.![(\frac{\sqrt[3]})'=-\frac})'}{(x^{\frac})^2}=-\frac}}}}=-4x^{-\frac}](https://tex.z-dn.net/?f=%28%5Cfrac%7B6%7D%7B%5Csqrt%5B3%5D%7Bx%5E2%7D%7D%29%27%3D-%5Cfrac%7B6%2A%28x%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D%29%27%7D%7B%28x%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D%29%5E2%7D%3D-%5Cfrac%7B4x%5E%7B-%5Cfrac%7B1%7D%7B3%7D%7D%7D%7Bx%5E%7B%5Cfrac%7B4%7D%7B3%7D%7D%7D%3D-4x%5E%7B-%5Cfrac%7B5%7D%7B3%7D%7D "(\frac{\sqrt[3]})'=-\frac})'}{(x^{\frac})^2}=-\frac}}}}=-4x^{-\frac}")
;
5.
;
6.
.
1.
2.
3.
4.
5.
6.
198–ой:
1.
2.
3.
4.
5.
6.
0
·
Хороший ответ
5 апреля 2023 05:40
Остались вопросы?
Еще вопросы по категории Алгебра
Найдите площадь ромба, сторона которого равна 50 см, а разность диагоналей - 20 см....
Решите задачу плизз В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсм...
Найдите наименьшее значение функции y =( x -8) e x -7 на отрезке [6;8]....
Упростите выражение: 1) (-а)2*а3 (2- вторая степень, 3- третья степень) 2) -а2*а3 (2- вторая степень, 3- третья степень) 3)а2*(-а)3 (2- вторая степень...
Решите уравнение: а)sin x/4 = 1/2 ; б) tg(-4x) = 1/ (корень)3 ; в) 2 sin (3x - П/4)= - корень 2 ; г) 2 sin ( П/3- x/4) = корень 3. ПОМОГИИИТЕ НАРОООД...
Все предметы 
