Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 05:52
826
уравнение окружности с центром в точке пересечения графиков функций y=√5-x и y=2^x и радиус r=1/2 имеет. вид.
2
ответа
Уравнение окружности с центром в точке (x₀;y₀) и радиусом r имеет вид:
(x-x₀)²+(y-y₀)²=r²
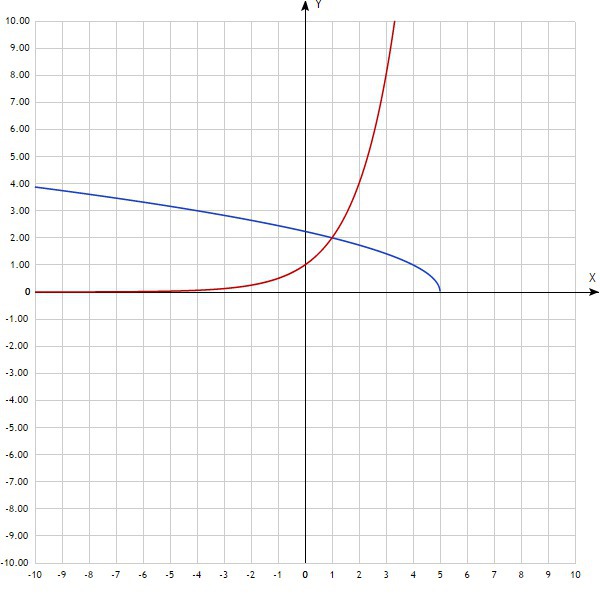
Найдём координаты центра окружности, для этого начертим чертёж графиков функций и по нему определим точки пересечения. Точка пересечения графиков имеет координаты (1;2). Следовательно уравнение окружности примет вид
(x-1)²+(y-2)²=(1/2)²
x²-2x+1+y²-4y+4=1/4
x²+y²=1/4-1-4+2x+4y
x²+y²=2x+4y-4(3/4)
(x-x₀)²+(y-y₀)²=r²
Найдём координаты центра окружности, для этого начертим чертёж графиков функций и по нему определим точки пересечения. Точка пересечения графиков имеет координаты (1;2). Следовательно уравнение окружности примет вид
(x-1)²+(y-2)²=(1/2)²
x²-2x+1+y²-4y+4=1/4
x²+y²=1/4-1-4+2x+4y
x²+y²=2x+4y-4(3/4)
0
·
Хороший ответ
5 апреля 2023 05:52
Строим график функции  :
:
1) Строим график функции ,
,

2) Симметрично отображаем график фенкции относительно оси Oy, получаем график
относительно оси Oy, получаем график  ,
,
3) Переносим ось Oy влево на 5 единиц, получаем график .
.
В этой же системе координат строим график :
:

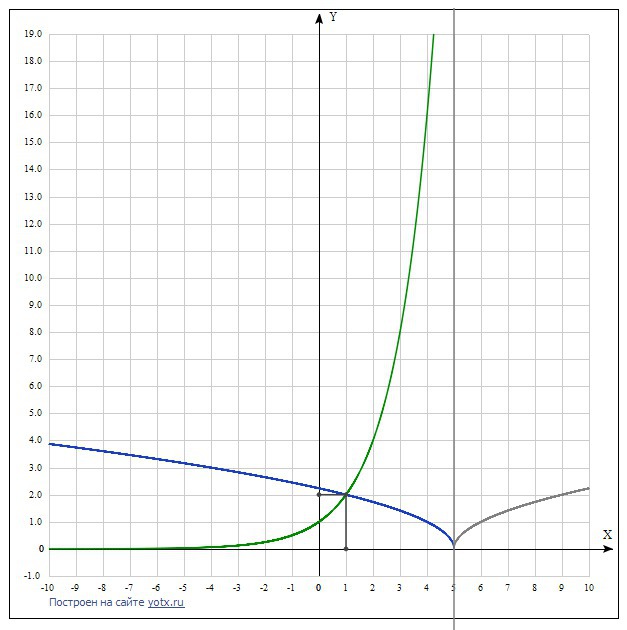
(1;2) - точка пересечения графиков.
Уравнение окружности:

1) Строим график функции
2) Симметрично отображаем график фенкции
3) Переносим ось Oy влево на 5 единиц, получаем график
В этой же системе координат строим график
(1;2) - точка пересечения графиков.
Уравнение окружности:
0
5 апреля 2023 05:52
Остались вопросы?
Еще вопросы по категории Математика
Расстояние между двумя станциями 784 км. Одновременно вышли навстречу друг другу 2 поезда. Они встретились через 8 часов. Найдите скорость каждого пое...
между учениками 5 класса полилили поровну по 279 учебников и 93 наклейки .сколько учеников в классе?...
Какое количество блокнотов указано в задании?...
Какой объем жидкости получится, если умножить 1 дм3 25 см3 на 16?...
Какие вопросы обсуждались на аудиенциях, проведенных фараоном?...