Найдите углы ромба с диагоналями 2√3 и 2

1 ответ

Посмотреть ответы

DevAdmin

1720

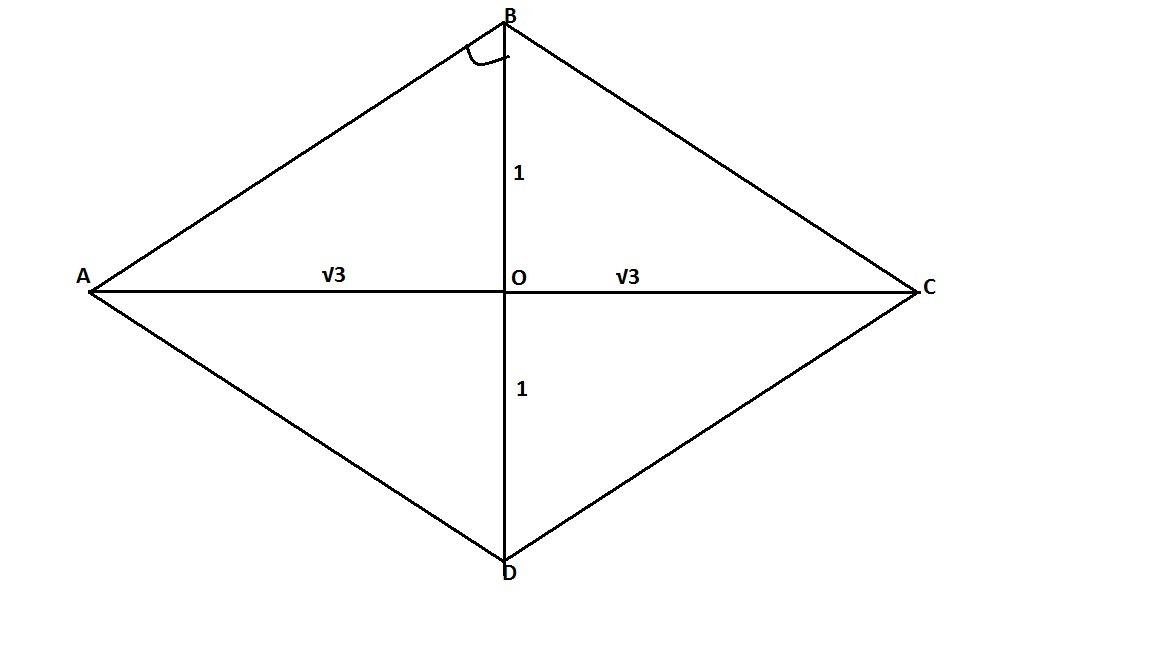
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
Рассмотрим один из треугольников, образованного пересечением диагоналей.
Он прямоугольный и его катеты равны √3 и 1.
По теореме Пифагора:
$AB = \sqrt = \sqrt = 2$
Значит, $OB = \dfracAB$ ⇒ ∠BAC = 30°, т.к. напротив угла в 30° лежит катет, равный половине гипотенузы.
∠BAD = 2 · 30° = 60°, т.к. диагонали ромба являются биссектрисами его углов.
∠ABO = 90° - 30° = 60°
∠ABC = 2 · 60° = 120°
∠ABC = ADC = 120° и ∠BAD = ∠BCD = 60° - как противоположные углы
Ответ: 60°, 120°, 60°, 120.°.

Хороший ответ

5 апреля 2023 07:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, точка K – середина DC. 1.Каково взаимное рас... Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна 360 см^2. Высота пирамиды проходит через точку пере... Чему равна площадь равностороннего треугольника,высота которого 9 см?... одно из оснований трапеции равно 28 высота равна 8 а площадь равна 178.найти второе основание трапеции... Фонарь закреплен на столбе на высоте 5,4. Человек стоит на расстоянии 6 км от столба и отбрасывает тень длиной 3 м. Каково роста человек?...