С1 Решить уравнение (1/2)sin2x+sin^2x-sinx=cosx И указать корни уравнения на отрезке [-2π;-π/2]

2 ответа

Посмотреть ответы

d.scherbetov

$\dfrac sin2x+sin^2x-sinx=cosx\\ \dfrac \cdot 2sin xcosx+sin^2x-sin x - cos x =0\\ sinx(cosx + sinx) - (sinx + cos x) = 0\\ (sinx - 1)(cos x + sin x) = 0\\ 1)~~sin x - 1 = 0; ~~~sin x = 1; ~~~ \boxed +2\pi n, n \in Z} \\$
$2)~~ cos x + sin x = 0; ~~~\big| \cdot \dfrac{\sqrt} \\\dfrac{\sqrt}cos x + \dfrac{\sqrt}sinx = 0 \\ \\ sin\dfrac{\pi}\cdot cosx +cos\dfrac{\pi } \cdot sin x=0\\ \\ sin(x+\dfrac{\pi })=0\\ \\ x+\dfrac{\pi }=\pi k;~~\boxed+\pi k,k \in Z}$
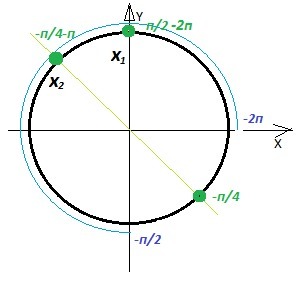
Kорни уравнения на отрезке [-2π;-π/2]. Выбор корней на единичной окружности.
x₁ = -3π/2; x₂ = -5π/4;

Хороший ответ

1 сентября 2022 21:19

Megamozg

2205

$\tt \frac \sin 2x+\sin^2x-\sin x=\cos x\\ \\ \frac \cdot 2\sin x\cos x+\sin^2x-\sin x-\cos x=0\\ \\ \sin x\cos x+\sin^2x-\sin x-\cos x=0\\ \\ \sin x(\cos x+\sin x)-(\cos x+\sin x)=0\\ \\ (\cos x+\sin x)(\sin x-1)=0$
Произведение равно нулю, если хотя бы один из множителей равен нулю
$\tt \sin x+\cos x=0$ (*)
При х=π/2 имеет 1=0 - не верно, значит имеем право разделить левую и правую части уравнения (*) на cosx≠0.
$\tt tgx=-1\\ \\ \boxed{\tt x=-\frac{\pi} +\pi n,n \in \mathbb}\\ \\ \sin x-1=0\\ \sin x=1\\ \\ \boxed{\tt x=\frac{\pi}+2\pi k,k \in \mathbb}$

Отбор корней на отрезке [-2π;-π/2].
1. Если n=-1, то $\boxed{\tt x=-\frac{\pi} -\pi =-\frac}$
2. Если k=-1, то $\boxed{\tt x=\frac{\pi} -2\pi =-\frac}$

1 сентября 2022 21:19

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Постройте график функции y=3x-2... Здравствуйте! Помогите решить! даю 50 баллов изобразите схематически график функции, заданной формулой вида y=kx+b, если а)k>0,b>0 б)k<0,b&... Семен решал квадратное уравнение 3x2+bx+c=0 и обнаружил, что два его корня — это числа tg α и 3ctg α при некотором α. Найдите c.... А) Найдите разность арифметической прогрессии: 1,8; 4,1; 6,4... б) найдите знаменатель геометрической прогрессии 1,5;-4,5;13,5;...... Сумма вертикальных углов MOE,POK,образованных при пересечении прямых MK и PE равна 198 градусов.Найдите угол MOP Помогите нубу)...