Докажите что , если медиана треугольника равна половине стороны , к которой она проведена , то треугольник прямоугольный.

1 ответ

Посмотреть ответы

Megamozg

2205

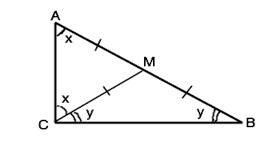
Пусть в ∆ АВС отрезок СМ - медиана и по условию СМ=АМ=ВМ. Тогда ∆ АМС и ∆ ВМС - равнобедренные с равными углами при основаниях. Примем ∠МАС=∠МСА=х, и ∠МСВ=МВС =у
Сумма углов треугольника 180° ⇒ 2х+2у=180° ⇒ х+у=90°. Тогда ∠АСВ=х+у=90°. ⇒ ∆ АВС - прямоугольный. Доказано.

Хороший ответ

5 апреля 2023 11:04

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Помогитеее!!! Высоты,проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС,пересекаются в точке М.Найдите углы треуго... высота цилиндра равна 8 см, радиус основания 5 см, на расстоянии 4 см от оси цилиндра параллельно ей проведено сечение, найти площадь этого сечения... Какое из следующих утверждений верно? 1)В прямоугольном треугольнике гипотенуза равна сумме катетов 2) Один из двух смежных углов острый а другой тупо... Выведите формулу для вычисления угла правильного n-угольника... Дано абсд трапеция угол а 60 градусов угол д 45 градусов бс 3 найти ад площадь абсд угол ф и угол е по 90 градусов...