Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно, 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей. Только не теоремой Герона, решить как за 8 класс.

1 ответ

Посмотреть ответы

DevAdmin

1720

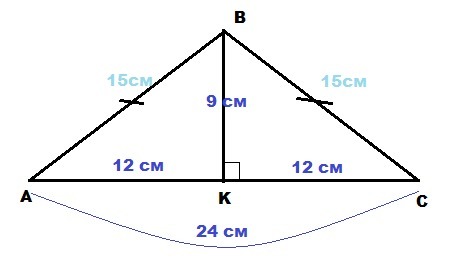
ΔABC - равнобедренный : AB = BC;
AC = 24 см; BK⊥AC; BK = 9 см
ВК - высота равнобедренного треугольника, она же и медиана ⇒
АК = КС = АС : 2 = 24 : 2 = 12 см
По теореме Пифагора из прямоугольного ΔВСК :
BC² = BK² + KC² = 9² + 12² = 225 = 15²
BC = 15 см ⇒ AB = BC = 15 см

Площадь треугольника АВС можно посчитать с помощью трех разных формул
1) Через основание и высоту
$S_=\frac =\frac =108$ см²

2) Через полупериметр и радиус вписанной окружности
$S_ = pr = \dfrac*r=\dfrac *r=27r$
27r = 108 ⇒ r = 108 : 27 = 4 см

3) Через 3 стороны и радиус описанной окружности
$S_=\dfrac \\ \\ R = \dfrac} =\dfrac =12,5$
R = 12,5 см

Ответ: радиус вписанной окружности r = 4 см;
радиус описанной окружности R = 12,5 см

Хороший ответ

1 сентября 2022 21:33

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Угол 1 - угол 2 = 75° Найти угол 1, угол 2, угол 3.... на рисунке: угол ВАЕ = 112 градусов, угол DBF = 68 градусам, ВС = 9 см. найдите сторону АС треугольника АВС... Угол между биссектрисой угла АОС и лучом, дополнительным к стороне ОС, равен 138 градусам. найдите угол АОС.... Диагональ боковой грани правильной треугольной призмы наклонена к плоскости основания под углом альфа, а площадь этой грани равна Q. Найдите площадь п... Угол ACO равен 28*, где O центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключённой внутри этого...