объясните, как построить сечение тетраэдра плоскостью, проходящей через данные точки М, N, К и в задачах 1-3 найти периметр сечения, если М, N, К – середины ребер и каждое ребро тетраэдра равно а.

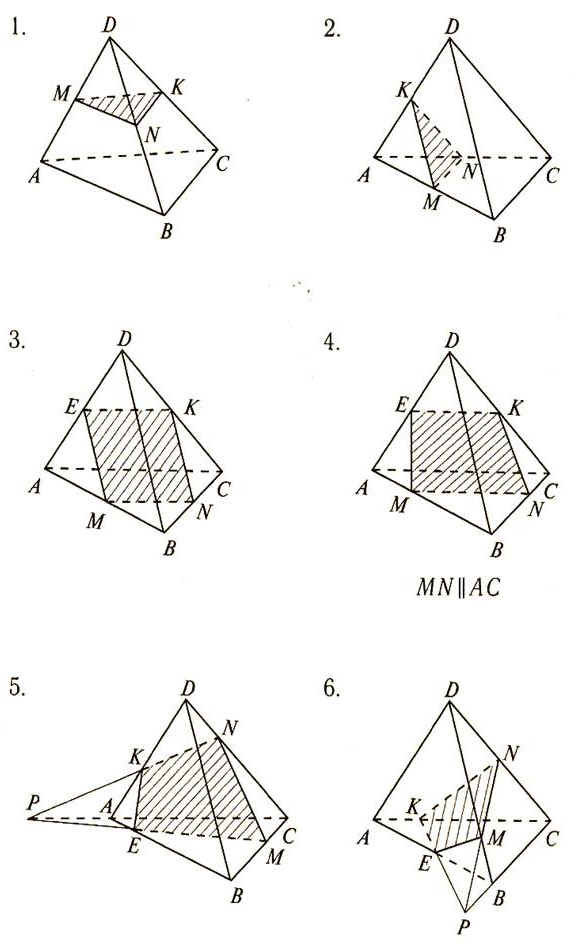
1. Точки M и N лежат в плоскости одной грани ABD. Соединяем их. MN - отрезок сечения.
Точки К и N лежат в плоскости одной грани BDС. Соединяем их. КN - отрезок сечения.
Точки M и К лежат в плоскости одной грани AСD. Соединяем их. MК - отрезок сечения.
MNK - искомое сечение.
Отрезки MN, KN и MK - средние линии соответствующих треугольников, значит MN = KN = MK = а/2.
Pmnk = 3 · a/2 = 3a/2

2. Построение аналогично заданию 1. Попарно соединяем точки M, N и К, так как каждая пара лежит в плоскости одной грани.
Отрезки MN, KN и MK - средние линии соответствующих треугольников, значит MN = KN = MK = а/2.
Pmnk = 3 · a/2 = 3a/2

3. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
KN║BD как средняя линия треугольника DBC, ⇒ KN║(ABD).
Секущая плоскость проходит через прямую KN и пересекает параллельную ей плоскость (ABD), значит линия пересечения будет параллельна KN.
Проводим ЕМ║BD, а так как KN║BD, то ЕМ║KN.
EMNK - искомое сечение.
ЕМ - средняя линия треугольника ABD, ⇒ ЕМ = а/2,
KN - средняя линия треугольника СBD, ⇒ KN = а/2,
ЕK - средняя линия треугольника ACD, ⇒ ЕK = а/2,
NМ - средняя линия треугольника ABC, ⇒ NМ = а/2,
Pemnk = 4 · a/2 = 2a

4. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
MN║AC, ⇒ MN║(ADC), секущая плоскость проходит через MN и пересекает (ADC), значит линия пересечения параллельна MN.
Проводим КЕ║АС, а так как MN║AC, ⇒ КЕ║MN.
EMNK - искомое сечение.

5. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
(АDC) ∩ (ABC) = АC. Прямые КN и АС лежат в одной плоскости, точка их пересечения - Р.
Точки М и Р лежат в одной плоскости (АВС), прямая МР пересекает ребро АВ в точке Е.
EMNK - искомое сечение.

6. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
(ВDC) ∩ (ABC) = ВC. Прямые МN и ВС лежат в одной плоскости, точка их пересечения - Р.
Точки К и Р лежат в одной плоскости (АВС), прямая КР пересекает ребро АВ в точке Е.
EMNK - искомое сечение.