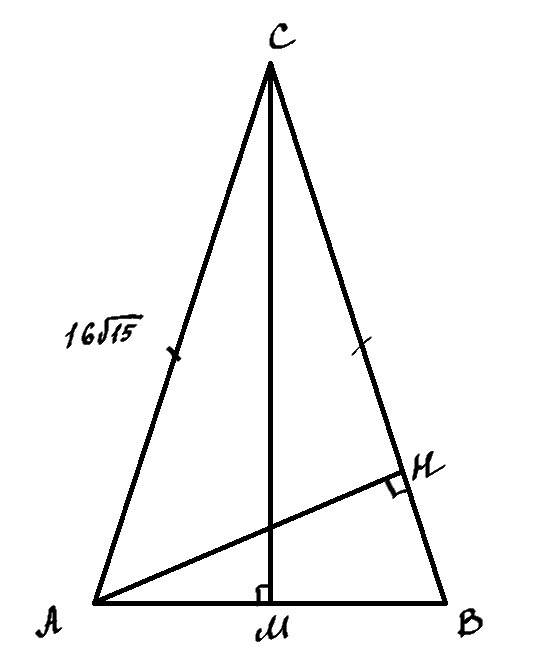
В равнобедренном треугольнике ABC с основанием AB боковая сторонаравна 16 корень из 15 , sin BAC = 0,25 .Найдите длину высоты AH.

1 ответ

Посмотреть ответы

DevAdmin

1720

Из вершины С проведем высоту к основанию. Обозначим ее СМ (см. рисунок).
Т.к. ΔАВС равнобедренный, то СМ будет являться и высотой, и медианой.

Рассмотрим ΔАСМ. Он прямоугольный.
sin∠ВАС = 0,25; АС=16√15 (по условию)

$sinBAC=\frac\\ \\0,25=\frac} \\ \\CM=0,25*16\sqrt=4\sqrt$

По теореме Пифагора найдем АМ.

$AM=\sqrt=\sqrt{(16\sqrt)^2-(4\sqrt)^2}=\sqrt=\sqrt=60$

Рассмотрим ΔАBН. Он прямоугольный, т.к. АН⊥СВ.
АМ=МВ
АВ=2АМ=2*60=120

∠САВ=∠СВА, т.к. ΔАВС равнобедренный.
sin∠САВ=sin∠AВH=0,25

$sinABH=\frac\\ \\0,25=\frac\\ \\AH=0,25*120= 30$

Ответ: АН = 30

Хороший ответ

14 октября 2022 17:30

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Какая длина в метрах соответствует 0 15 мм?... Какой результат вычислений?... Постройте угол ABC =70 градусов и проведите его биссектрису.Какова градусная мера образовавшихся углов?... катер прошёл 22 км по течению реки и 5 км против течения затратив на весь путь 4ч.найдите скорость катера в стоячей воде ,зная, что скорость течения р... 4.Найдите значение выражений, применяя распределительное свойство умножения: а) 289 · 31 + 211 · 31; б) 647 · 243 – 243 · 447; в) 139 · 37 – 108 ·...