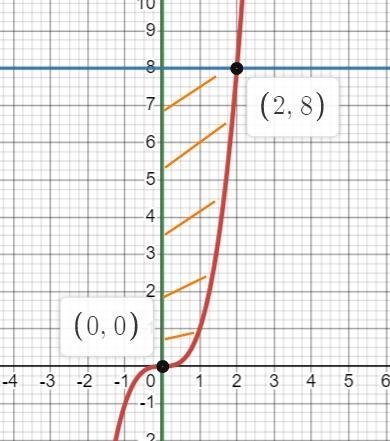
Найти площадь, ограниченная линиями
y=x^3
y=8
x=0

1 ответ

Посмотреть ответы

m.pozharskiy

Ответ:
площадь фигуры равна 12 кв. ед.
Пошаговое объяснение:
Делаем чертеж, определяемся по четрежу с фигурой, пределами интегрирования, функциями у₁(х) и у₂(х). За у₁(х) принимают функцию, график которой лежит "выше" на координатной плоскости в интервале интегрирования.
Затем используем формулу Ньютона-Лейбница
$\displaystyle S=\int\limits^a_b {\bigg(y_1(x)-y_2(x\bigg)} \, dx$
В нашем случае
а = 2
b = 0
у₁(х) = 8;
у₂(х) = x³.
Считаем площадь
$\displaystyle S=\int\limits^2_8 {\bigg(8-x^3\bigg)} \, dx=8x\bigg|_0^2-\frac \bigg|_0^2=16-4=12$
#SPJ1

Хороший ответ

11 ноября 2022 10:28

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Как называется число, равное '10 в минус 27 степени'?... Выразите углы в радианах а ) 45... ( корень из 5 + корень из 8) в квадрате - корень из 90. Можете рассказать как и показать... На каком рисунке изображено множество решений неравенства ×^2-6×-27>0... 3,5/4,8 : 7/8 + 4,4/3,9 * 3 целых 1/4= По действиям,если можно 26*0,8-20,44:2,8=. По действиям,если можно...

Найти площадь, ограниченная линиями y=x^3 y=8 x=0

Найти площадь, ограниченная линиями
y=x^3
y=8
x=0