Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
30 ноября 2022 02:56
1173
Найдите уравнение касательной, проведённой к графику функции f(x) в точку x0, если:f(x)=cos(1+4x), x0=-0,25
2
ответа
Уравнение касательной:
y = f ’(x0) * (x − x0) + f(x0).
Здесь f ’(x0) — значение производной в точке x0, а f(x0) — значение самой функции.
f '(x) = -4sin(1+4x).
f '(xo) = -4sin(1+4*(-0.25)) = -4sin(1-1) = 0.
f(x0) = cos(1+4*(-0.25)) = cos0 = 1.
Получаем уравнение касательной:
у = 0*(х - 0,25) + 1 = 1.
Ответ: уравнение касательной к графику функции
f(x)=cos(1+4x) в точке x0=-0,25 имеет вид у = 1.
Примечание: так как производная в заданной точке равна 0, то эта точка - критическая и касательная в этой точке - прямая, параллельная оси Ох.
y = f ’(x0) * (x − x0) + f(x0).
Здесь f ’(x0) — значение производной в точке x0, а f(x0) — значение самой функции.
f '(x) = -4sin(1+4x).
f '(xo) = -4sin(1+4*(-0.25)) = -4sin(1-1) = 0.
f(x0) = cos(1+4*(-0.25)) = cos0 = 1.
Получаем уравнение касательной:
у = 0*(х - 0,25) + 1 = 1.
Ответ: уравнение касательной к графику функции
f(x)=cos(1+4x) в точке x0=-0,25 имеет вид у = 1.
Примечание: так как производная в заданной точке равна 0, то эта точка - критическая и касательная в этой точке - прямая, параллельная оси Ох.
0
·
Хороший ответ
2 декабря 2022 02:56
Применены правила дифференцирования, общий вид уравнения касательной
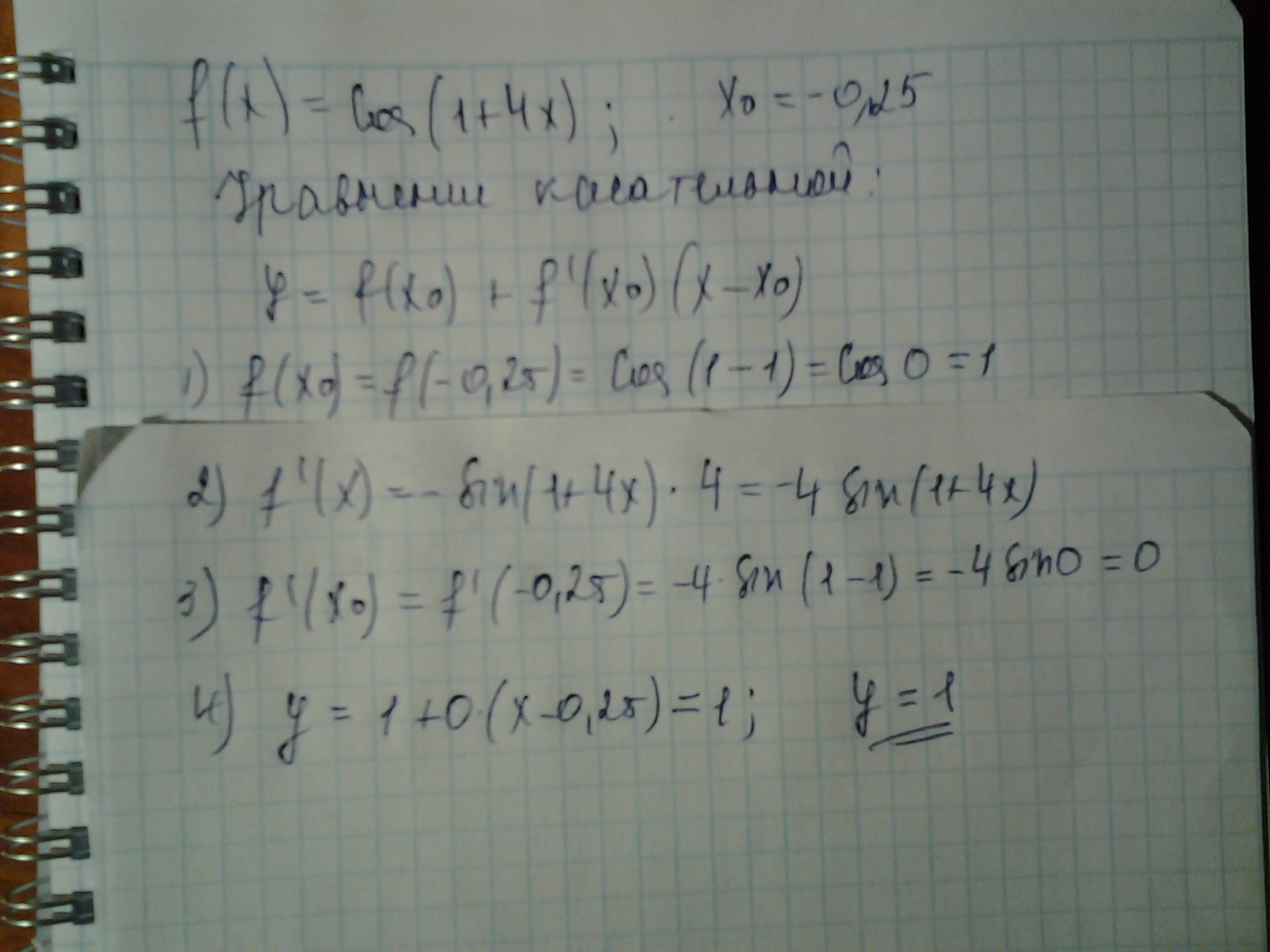
0
2 декабря 2022 02:56
Остались вопросы?
Еще вопросы по категории Математика
Найти производную y=4 Как вы это сделали , объясните пожалуйста...
Что такое 10 в минус седьмой степени?...
Раскройте скобки: а) (x+y-z)*3 б) 4*(m-n-p) в) -8*(a-b-c) г) (2x-y+3)*(-2) д) (3m-2n+p)*(-1) е) (a+5-b-c)*m...
Напишите: а)все чётные числа,большие 10 и меньшие 21 б)все не чётные числа,большие 12,но меньшие 23. НАпишите пожалуйста как решали тоесть решение!...
Множитель множитель произведение 2 помогите пожалуйста решить пример...