Найдите промежутки возрастания и убывания функции.

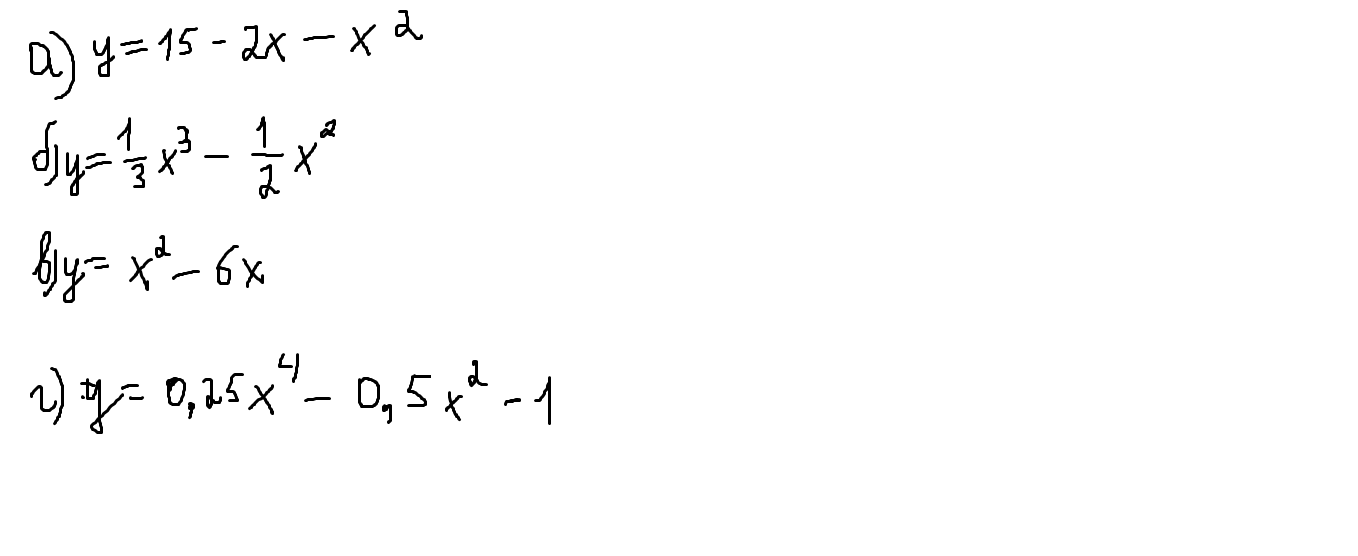
1 ответ

Посмотреть ответы

Megamozg

2205

a) $y=15-2x-x^2\\ y'=-2-2x\\ -2-2x=0\\ 2x=-2\\ x=-1\\$
ставим точку -1 на сисловой прямой. и смотри на уравнение y=-2-2x. знак перед отрицательый, значит __+_-1_-__. Т.е. начинаем не сплюса, как обычно, а с минуса, т.е. перед иском минус.
$(-\infty;-1)$ - промежуток возрастания
$(-1;+\infty)$ - промежуток убывания

б) $y=\fracx^3-\fracx^2\\ y'=x^2-x\\ x^2-x=0\\ x(x-1)=0\\ x=0\\ x-1=0\\ x=1$
отмечаем точки 0 и 1 на числовой примой. уравнение x^2-x. смотрим на иск со старшей степенью - x^2 - положительный. значит расставляем знаки с плюса, чередуя(если же сомнения возникают, то можно делать проверки уравнения x^2-x промежуточных значений и смотреть какой знак выходит, так уж не ошибёшься). выходит: _+_0_-_1_+_
$(-\infty;0)\cup(1;+\infty)$ - промежутки возрастания
$(0;1)$ - промежуток убывания

в) $y=x^2-6x\\ y'=2x-6\\ 2x-6=0\\ 2x=6\\ x=3\\$
Снова те же операции, отмечаем 3-ойку. 2x-6 - соотвественно начинаем с плюса, чередуя. _-_3_+_
$(3;+\infty)$ - промежуток возрастания
$(-\infty;3)$ - промежуток убывания

г) $y=0,25x^4-0,5x^2-1\\ y'=x^3-x\\ x^3-x=0\\ x(x^2-1)=0\\ x=0\\ x^2-1=0\\ x^2=1\\ x=\pm 1$
точки -1, 0, 1. уравнение x^3-x. у иска со старшей степенью знак положительный, начинаем с плюса и чередуем
_-_-1_+_0_-_1_+_
$(-1;0)\cup(1;+\infty)$ - промежутки возрастания
$(-\infty;-1)\cup(0;1)$ - промежутки убывания

Хороший ответ

2 декабря 2022 04:12

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Найдите производную функции y=1/x^2... в сосуд, имеющий форму конуса, налили 30 мл жидкости до половины высоты сосуда. Сколько мл жидкости нужно долить в сосуд, чтобы заполнить его доверху?... Представьте в виде многочлена 1)33.1 2) 33.2 3)33.3... Найдите значение выражения (8b−8)(8b+8)−8b(8b+8) при b=2,6.... Упростите выражение tga/1-tg^2a...