Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
30 ноября 2022 04:51
8249
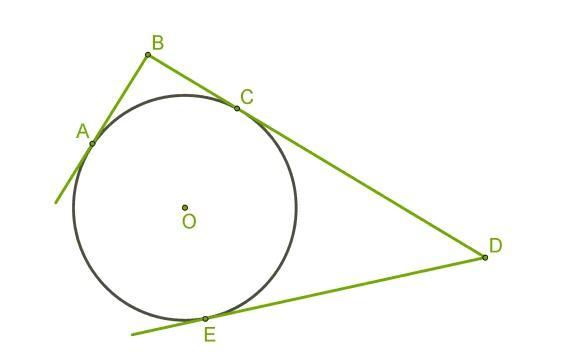
Проведены касательные к окружности AB, BD и DE так, что A, C и E — точки касания. Длина ломаной ABDE равна 54,3 см.Определи длину отрезка DB.
Ответ: DB = (см)
1
ответ
Ответ:
По свойству отрезков касательных, проведенных к окружности, а именно, отрезки касательных, проведенных к окружрости из одной точки равны. DC=DE и AB=BC
Значит, 54,3=2DC+2BC=2(DC+BC)=2DB.
Следовательно, DB=54,3:2=27,15
По свойству отрезков касательных, проведенных к окружности, а именно, отрезки касательных, проведенных к окружрости из одной точки равны. DC=DE и AB=BC
Значит, 54,3=2DC+2BC=2(DC+BC)=2DB.
Следовательно, DB=54,3:2=27,15
0
·
Хороший ответ
2 декабря 2022 04:51
Остались вопросы?
Еще вопросы по категории Геометрия
1) На данном рисунке OC- биссектриса угла AOB, угол 1= 128 градуса, угол 2= 52 градуса. а) Докажите, что AO=AC б) Найдите угол ACO 2) Дан угол ABC, ра...
Равные углы это........,...
в основании прямой треугольной призмы abca1b1c1 лежит равнобедренный треугольник ABC с основанием BC,равным 4,и боковой стороной длиной 5.площадь сече...
Начертите неравнобедренный треугольник ABC с верхней вершиной B. Проведите из венршины B медиану, а из вершины A- биссектрису...
На биссектрисе угла А взята точка D, а на сторонах этого угла - точки В и С такие, что угол ADB равен углу DCA. Доказать, что треугольник ABD рав...