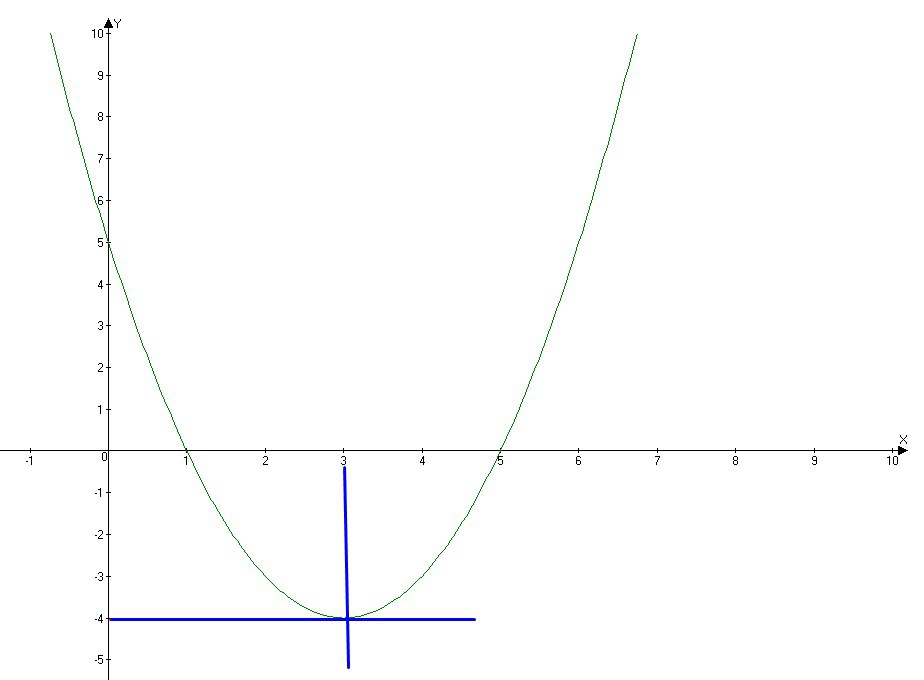
Постройте график функции y=x^2 - 6x + 5. Найдите с помощью графика:а)значение y при x=0.5
б)значения x при которых y=-1
в)нули функции; промежутки, в которых y>0 и в которых y<0
г)промежуток на котором функция возрастает.

1 ответ

Посмотреть ответы

Megamozg

2205

Найдем вершину параболы

$x=- \frac =- \frac{-6} =3$

$y=3^2-6\cdot3+5=-4$

(3;-4) - координаты вершины параболы.

а) Найдем значение у при х=0,5

$y(0.5)=(0.5)^2-6*0.5+5=2.25$

б) Значения х при у=-1
$-1=x^2-6x+5\\ x^2-6x+6=0\\ D=b^2-4ac=36-24=12\\ \\ x_1_,_2= \dfrac{-b\pm \sqrt } = \dfrac } =3\pm \sqrt$

в) Нули функции, промежутки, в которых y>0 и y<0
$x^2-6x+5=0$
По т. Виета: $x_1=5;\,\,\,\,\,x_2=1$ - нули функции
$y\ \textgreater \ 0$ , т.е. $x^2-6x+5\ \textgreater \ 0$
По графику $y\ \textgreater \ 0$ это будет промежутки $x\ \textless \ 1;\,\,\,x\ \textgreater \ 5$ , а $y\ \textless \ 0$ , т.е. $x^2-6x+5\ \textless \ 0$ это будет промежуток $1\ \textless \ x\ \textless \ 5$

г) Промежуток в котором функция возрастает - $x \in (3;+\infty)$

Хороший ответ

12 декабря 2022 11:17

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

упростите выражение ........ Докажите тождество 1)(a-b)(a+b)(a2+b2)= a4-b4 2)(a4+b4)(a4+b2)(a+b)(a-b)=a8-b8 #466... С 1 номера по 4 пожалуйста, очень нужно❤️... Дана арифметическая прогрессия: 33; 25; 17; … . Найдите первый отрицательный член этой прогрессии.?... найдите корень уравнения sin* pi(8x+9)/3=корень из 3/2. В ответе напишите наибольший отрицательный корень....