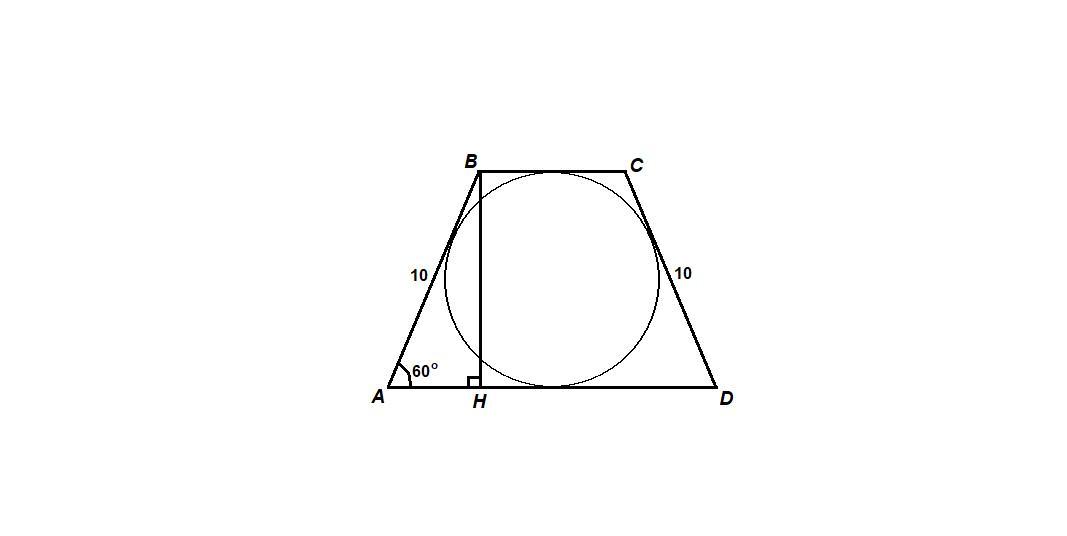
Боковая сторона равнобокой трапеции равна 10 см, а острый угол — 60°. Найдите площадь трапеции, если известно, что в неё можно вписать окружность.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ: 50√3 см²

Объяснение:
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны:
AD + BC = AB + CD = 10 · 2 = 20 см
ΔАВН: ΔAHB = 90°
sin∠A = BH/AB
BH = AB · sin∠A = 10 · sin60° = 10 · √3/2 = 5√3 см
Sabcd = 0,5 · (AD + BC) · BH = 0,5 · 20 · 5√3 = 50√3 см²

Хороший ответ

12 декабря 2022 17:49

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Помоогите срочно Биссектриса равностороннего треугольника равна половине стороны треугольника.Это утверждение... 1.может быть верно 2.верно всегда 3.н... В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF? причем EF=13 см. Найдите расстояние от точки F до прямой DE. Срочно!!... Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см.Найдите расстояние от точки М до плоскости АВС,если АВ=6 см... Двор состоит из пяти равных квадратов. Определи площадь двора в квадратных метрах, если периметр двора — 2520 см.... Боковая сторона трапеции равна 7 и 12 см Чему равен периметр трапеции если в нее можно вписать окружность...