Исследовать функцию с помощью производной и построить ее график y=x^3-3x^2+4 помогите пожалуйста

ДАНО
Y = x³ - 3*x² + 4
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y= (x-2)²(x+1). Корни: х₁,₂ = 2, х₃ = -1.
3. Пересечение с осью У. У(0) = 4.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальной асимптоты - нет.
5. Исследование на чётность.Y(-x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² - 6*х = 3*х*(х - 2) 0 .
Корни: х₁=0 , х₂ = 2.
Схема знаков производной.
_ (-∞)__(>0)__(x1=0)___(<0)___(x2=2)__(<0)_____(+∞)__
7. Локальные экстремумы.
Максимум Ymax(-1)= 4, минимум – Ymin(2)=0.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;0)∪(2;+∞) , убывает = Х∈(0;2).
8. Вторая производная - Y"(x) = 6*(x - 1)=0.
Корень производной - точка перегиба Y"(1)= 0.
9. Выпуклая “горка» Х∈(-∞;1), Вогнутая – «ложка» Х∈(1;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(oo)Y(x)/x. b = lim(oo)Y(x) – k*x. Наклонной асимптоты - нет
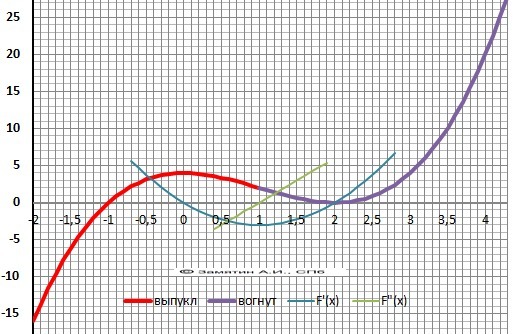
12. График в приложении.