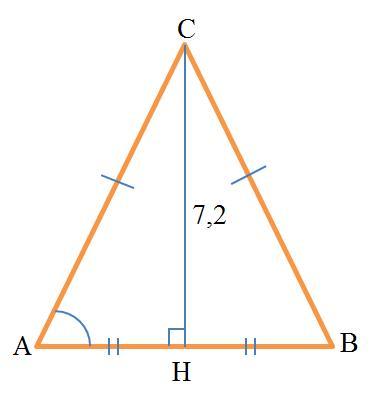
В треугольнике ABC AC = BC, высота CH равна 7,2 и cosA=4/5 . Найдите AC.

Ответ:
12 (единиц)
Объяснение:
Дано:
ΔABC (см. рисунок)
AC=BC
CH⊥AB
CH=7,2
cos∠A=4/5
Найти AC.
Решение.
Так как AC=BC, то ΔABC равнобедренный. Тогда углы ∠A и ∠B при основании равны, следовательно острые. Поэтому sin∠A > 0.
Далее, из cos∠A=4/5 получаем, что
sin∠A=√(1-cos²∠A) = √(1-16/25) = √(9/25) = 3/5.
С другой стороны sin∠A= CH/AC .
Отсюда
AC = CH/sin∠A = 7,2/(3/5) = (5∙7,2)/3 = 36/3 = 12 (единиц).