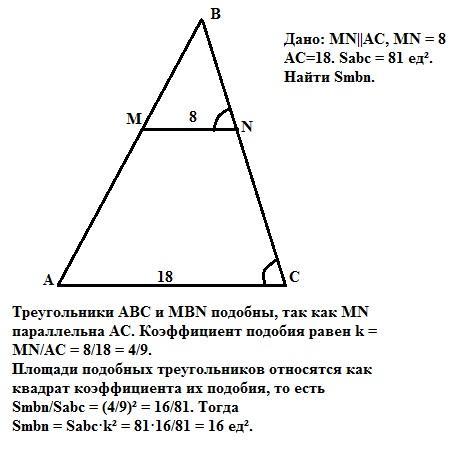
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно, АС-18,MN-8.Площадь треугольника АВС равна 81.Найдите площадь треугольника MBN

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
Smbn = 16 ед².
Объяснение:
Треугольники АВС и МBN подобны по двум углам, так как MN параллельна АС и ∠А = ∠М, как соответственные при параллельных прямых, а ∠В - общий. Тогда коэффициент подобия равен
k = MN/AC = 8/18 = 4/9.
Площади подобных треугольников относятся как квадрат коэффициента их подобия, то есть Smbn/Sabc = k² =(4/9)² =16/81. Тогда
Smbn = Sabc·k² = 81·16/81 = 16 ед².

Хороший ответ

16 декабря 2022 22:29

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

На расстоянии 4 см от центра шара проведено сечение,длина окружности которого равна 6П см. Найдите объём шара.С рисунком... в прямоугольном параллелепипеде abcda1b1c1d1 известны длины ребер AB 3 AD 4 AA1 32. Найдите площадь сечения, проходящего через вершины СС1 и А... Сколько осей симметрии имеет прямоугольник не являющийся квадратом? 1. Ни одной 2. Одну 3. Две 4. Четыре... Точка B принадлежит отрезку AC. AB=14, BC=6. Найдите длину отрезка MN, если M и N середины отрезков AB и BC... концы отрезка отстоят от плоскости а на расстояниях 12 и 8 см. найдите расстояние от середины отрезка до плоскости а....