Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 декабря 2022 02:05
719
Изменить порядок интегрирования в двойном интеграле
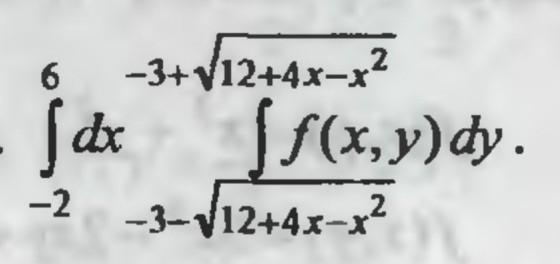
1
ответ
Ответ:
Изменить порядок интегрирования .
.
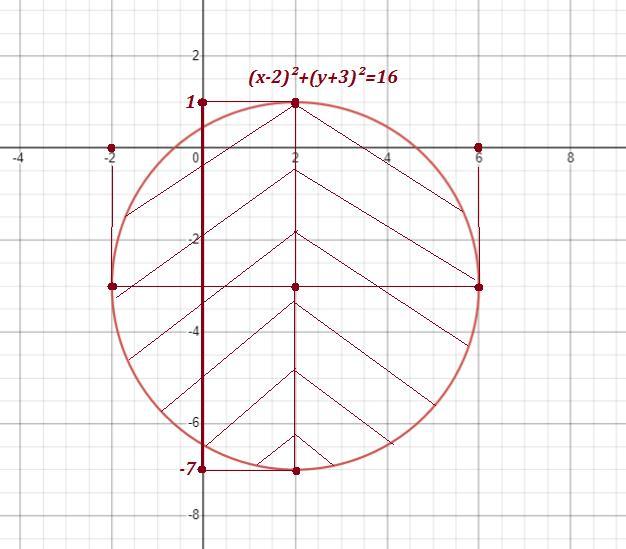
Область проецируется на ось ОХ в отрезок [-2 ; 6 ] .
Если начертить луч, параллельный оси ОУ, то точка входа в область лежит на кривой, уравнение которой имеет вид
 . Точка выхода из области лежит на кривой, уравнение которой имеет вид
. Точка выхода из области лежит на кривой, уравнение которой имеет вид
 . Это нижняя и верхняя полуокружности от
. Это нижняя и верхняя полуокружности от
окружности . Действительно,
. Действительно,

Это окружность с центром в точке (2;-3) и радиуса R=4 .
Выразим из уравнения окружности переменную х .

Последнее равенство - это правая (если знак +) и левая (если знак минус ) полуокружности от окружности .
.
Окружность проецируется на ось ОУ в отрезок [-7; 1 ] .

Изменить порядок интегрирования
Область проецируется на ось ОХ в отрезок [-2 ; 6 ] .
Если начертить луч, параллельный оси ОУ, то точка входа в область лежит на кривой, уравнение которой имеет вид
окружности
Это окружность с центром в точке (2;-3) и радиуса R=4 .
Выразим из уравнения окружности переменную х .
Последнее равенство - это правая (если знак +) и левая (если знак минус ) полуокружности от окружности
Окружность проецируется на ось ОУ в отрезок [-7; 1 ] .
0
·
Хороший ответ
17 декабря 2022 02:05
Остались вопросы?
Еще вопросы по категории Математика
хорда окружности, равная 6/π, стягивает дугу в 60°. найти длину этой дуги....
Сколько будет 1 от 500000 рублей?...
Помогите решить уравнения 2 класса. х-9=4,у+7=15,35-х=30...
На прямоугольный стол размера x×90 кладут одинаковые листы бумаги размера 6×10. Первый лист примыкает к левому нижнему углу, а каждый следующий кладут...
1 8 мм это сколько см?...