Х-множество натуральных чисел.Указаны два свойства. 1 св-во:"быть целым числом" 2св-во:"быть рациональным числом" На какие классы произошло разбиение множества Х. Укажите их. ПОМОГИТЕ ПОЖАЛУЙСТА

Натуральные числа - это числа, возникающие естественным образом при счете, например 1,2,3...и т.д.
Целые числа - это расширение множества натуральных чисел N, получаемое добавлением к N нуля и отрицательных чисел вида -n (такие же, как натуральные, но с минусом).
Все ли натуральные числа обладают свойством: быть целым числом? Да. Это видно из определения. Значит, подмножество Х1, выделенное из множества Х при помощи свойства "быть целым числом", равно множеству Х.
Рациональные числа - это числа, представляемые обыкновенной дробью , где числитель m - целое число, а знаменатель n - натуральное число.
Все ли натуральные числа обладают свойством: быть рациональным числом? Да. Потому что любое натуральное число х можно представить в виде дроби . Значит, подмножество Х2, выделенное из множества Х при помощи свойства "быть рациональным числом", равно множеству Х.
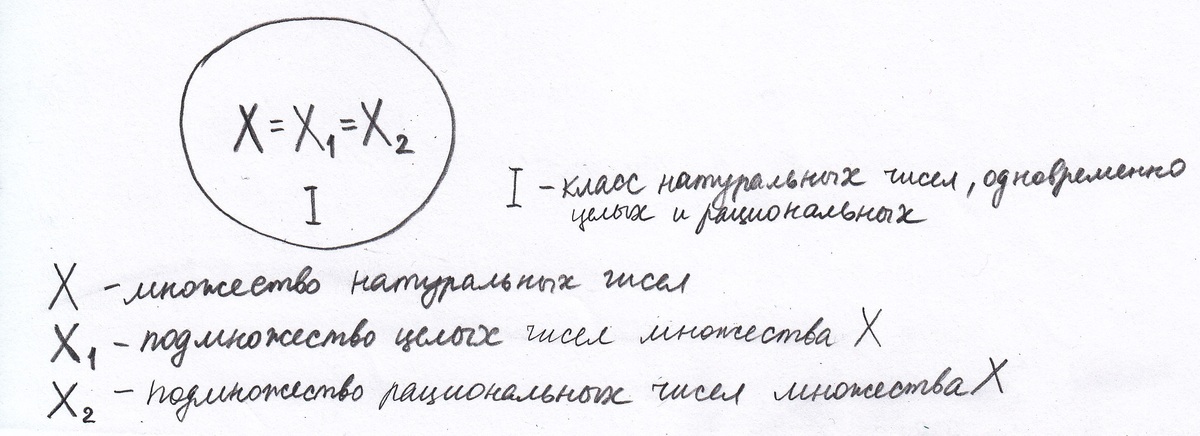
Таким образом, все элементы множества Х удовлетворяют каждому из свойств 1 и 2, значит, множество Х разбивается на I класс - класс натуральных чисел, одновременно целых и рациональных.