Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 декабря 2022 08:17
529
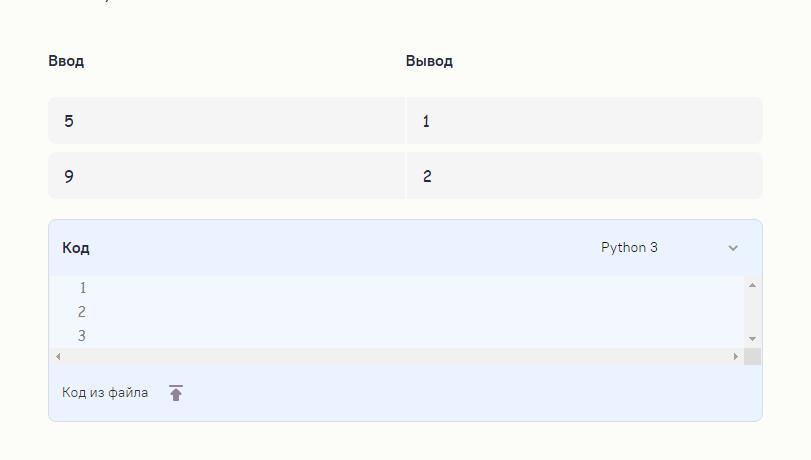
Лягушка и кузнечикОграничение по времени: 0.5 секунды
В крайних клетках полоски шириной в одну клетку и длиной в N клеток сидят лягушка и кузнечик: лягушка в клетке под номером 1, кузнечик в клетке под номером N. Каждую секунду лягушка прыгает в сторону кузнечика, и одновременно кузнечик прыгает в сторону лягушки. Лягушка может прыгать только на две или на три клетки, кузнечик — только на одну или на две клетки. За какое наименьшее время они смогут оказаться в одной клетке?
Формат входных данных
Единственная строка входных данных содержит целое число N — длину клетчатой полосы (2≤N≤2⋅109).
Формат выходных данных
Если лягушка и кузнечик могут оказаться в одной клетке, требуется вывести одно целое число — минимальное количество секунд, через которое они могут встретиться. Если они не смогут оказаться в одной клетке, требуется вывести число «−1» (без кавычек).
Система оценки
Решения, правильно работающие при N≤30, будут оцениваться в 30 баллов.
Решения, правильно работающие при N≤105, будут оцениваться в 50 баллов.
Пояснение
В первом примере лягушка может прыгнуть из клетки 1 в клетки 3 и 4, а кузнечик может прыгнуть из клетки 5 в клетки 3 и 4. Поэтому через 1 секунду они могут оказаться в одной клетке.
Во втором примере лягушка и кузнечик могут встретиться через 2 секунды. Например, лягушка прыгает в клетку 3, затем в клетку 6, а кузнечик прыгает в клетку 8, затем в клетку 6.
1
ответ
Ответ:
N = int(input())
M = 1537
n = N - 1
l = -1
r = n
while l < r - 1:
m = (l + r) // 2
if n - 5 * m < M:
r = m
else:
l = m
s = r
n -= 5 * s
dist = [0] + [-1] * M
jumps = [3,4,5]
q = [0]
while q:
d = q.pop()
for i in range(3):
if d + jumps[i] < M and dist[d + jumps[i]] == -1:
dist[d + jumps[i]] = dist[d] + 1
q.append(d + jumps[i])
print(-1 if dist[n] == -1 else s + dist[n])
Объяснение:
N = int(input())
M = 1537
n = N - 1
l = -1
r = n
while l < r - 1:
m = (l + r) // 2
if n - 5 * m < M:
r = m
else:
l = m
s = r
n -= 5 * s
dist = [0] + [-1] * M
jumps = [3,4,5]
q = [0]
while q:
d = q.pop()
for i in range(3):
if d + jumps[i] < M and dist[d + jumps[i]] == -1:
dist[d + jumps[i]] = dist[d] + 1
q.append(d + jumps[i])
print(-1 if dist[n] == -1 else s + dist[n])
Объяснение:
0
·
Хороший ответ
17 декабря 2022 08:17
Остались вопросы?
Еще вопросы по категории Информатика
ПОМОГИТЕ ПОЖАЛУЙСТА С ЗАДАНИЕМ! В ходе телевизионного шоу проводится смс-голосование: каждый телезритель отдат свой голос за одного из 12 артистов-уча...
паскаль прошу очень важно)Напишите программу, которая в последовательности натуральных чисел определяет максимальное число, кратное 4. Программа получ...
приведите известные вам примеры иерархий из других предметных областей(биология,география,математика,история и т.д)...
Пирамидальная сортировка 34 31 22 16 29 28 11 27 17 28 38 33 17 29 10...
1. Минимально необходимый набор устройств для работы компьютера содержит… a) принтер, системный блок, клавиатуру b) системный блок, монитор, клавиа...