Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 декабря 2022 15:25
1139
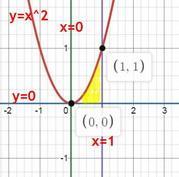
Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной линиями y=x2, x=0 и x=1, y=0 вокруг оси абсцисс
2
ответа
Ответ:
 кубических единиц
кубических единиц
Пошаговое объяснение:
Надо посчитать тройной интеграл. (чтобы не помнить никаких других формул)
пределы интегрирования:
y изменяется от 0 до ;
;
x изменяется от 0 до 1;
угол поворота α меняется от 0 до 2π (полный поворот)

Пошаговое объяснение:
Надо посчитать тройной интеграл. (чтобы не помнить никаких других формул)
пределы интегрирования:
y изменяется от 0 до
x изменяется от 0 до 1;
угол поворота α меняется от 0 до 2π (полный поворот)
0
·
Хороший ответ
17 декабря 2022 15:25
Ответ:
Пошаговое объяснение:
y=x², x₁=0 и x₂=1, y=0 вокруг оси абсцисс

сначала рисуем графики и сразу видим, что у нас получается "воронка"
у₁ = х²; у₂ = 0
итак, считаем определенный интеграл

Пошаговое объяснение:
y=x², x₁=0 и x₂=1, y=0 вокруг оси абсцисс
сначала рисуем графики и сразу видим, что у нас получается "воронка"
у₁ = х²; у₂ = 0
итак, считаем определенный интеграл
0
17 декабря 2022 15:25
Остались вопросы?
Еще вопросы по категории Математика
Сколько километров в одной версте?...
Раздели число 18 в отношении 1:2...
Нужен график y=sin 2x. Помогите!!!...
В саду растет 26 деревьев —— яблони и груши. Оказалось, что среди любых 18 деревьев обязательно есть хотя бы одна яблоня, а среди любых 10 деревьев ес...
на первом тракторе работали 60 ч на втором 55ч .на втором израсходавали на 35 л меньше горючего чем на первом . сколько литров горючего израсходавали...