Каждая грань куба разделена на 9 квадратиков. Какое самое большое число квадратиков можно покрасить, чтобы никакие два покрашенных квадратика не имели общей стороны.

1 ответ

Посмотреть ответы

DevAdmin

1720

В кубе 6 граней (сторон),
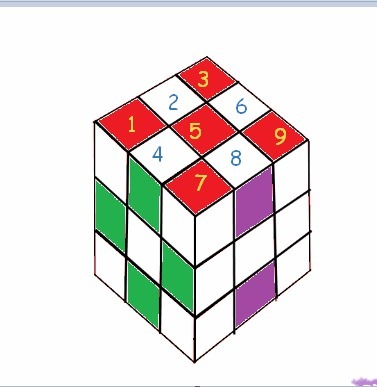
Каждая грань разделена на 9 кубиков, обозначим из по порядку:
1 2 3 4 5 6 7 8 9 (см. рисунок).
В купе 3 пары противоположных граней:
пара 1 - верняя и нижняя грани, раскрасим 5кубиков под номерами 1 3 5 7 9,
пара 2 - передняя и задняя грани, раскрасим 4 кубика под номерами 2 4 6 8
пара 3 - боковые грани, раскрасим 2 кубика под номерами 2 и 8.
Ответ: 1. условие выполнено - раскрашенные кубики не имеют общих сторон.
2. 2*5+2*4+2*2=22
Самое большое количество кубиков, которое можео покрасить соответственно условию, равно 22.

Хороший ответ

18 декабря 2022 00:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Митя приехал к другу и забыл код домофона от подъезда. Но часть цифр потёрты, от частоты использования. Какое наибольшее количество вариантов нужно ем... Обмотка тороида с немагнитным сердечником имеет 251 виток. Средний диаметр тороида 8 см, диаметр витков 2 см. На тороид намотана вторая обмотка со 100... На рисунке дано поле, расчерченное на квадраты со стороной 9 см. На нём изображена фигура. 9 см 9 см 1) Найдите периметр этой фигуры. Ответ дайте в... Какие 10 бсп предложений можно использовать в мотивационном письме?... Какова концентрация вещества, если в 1 кубическом сантиметре содержится 1 микромоль, а объем раствора составляет 100 микролитров?...