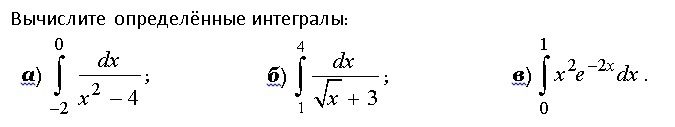Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
1)Несобственный интеграл 2-го рода (бесконечный разрыв в точке x=-2)


Интеграл расходится
2)

3)


Интеграл расходится
2)
3)
0
·
Хороший ответ
18 декабря 2022 02:16
Остались вопросы?
Еще вопросы по категории Математика
Какие значения могут принимать символы 1 и 0?...
Как перевести 10 метров в час?...
задача по математике 3класс мама заготовила 6 трёхлитровых банок яблочного сока и 9 таких же банок вишнёвого . Сколько всего литров сока заготовила ма...
Какой буквой обозначается длина окружности? ...
Каково расстояние, которое пройдет объект со скоростью 4 км/ч за 3 часа?...