Изменить порядок интегрирования и вычислить двойной интеграл

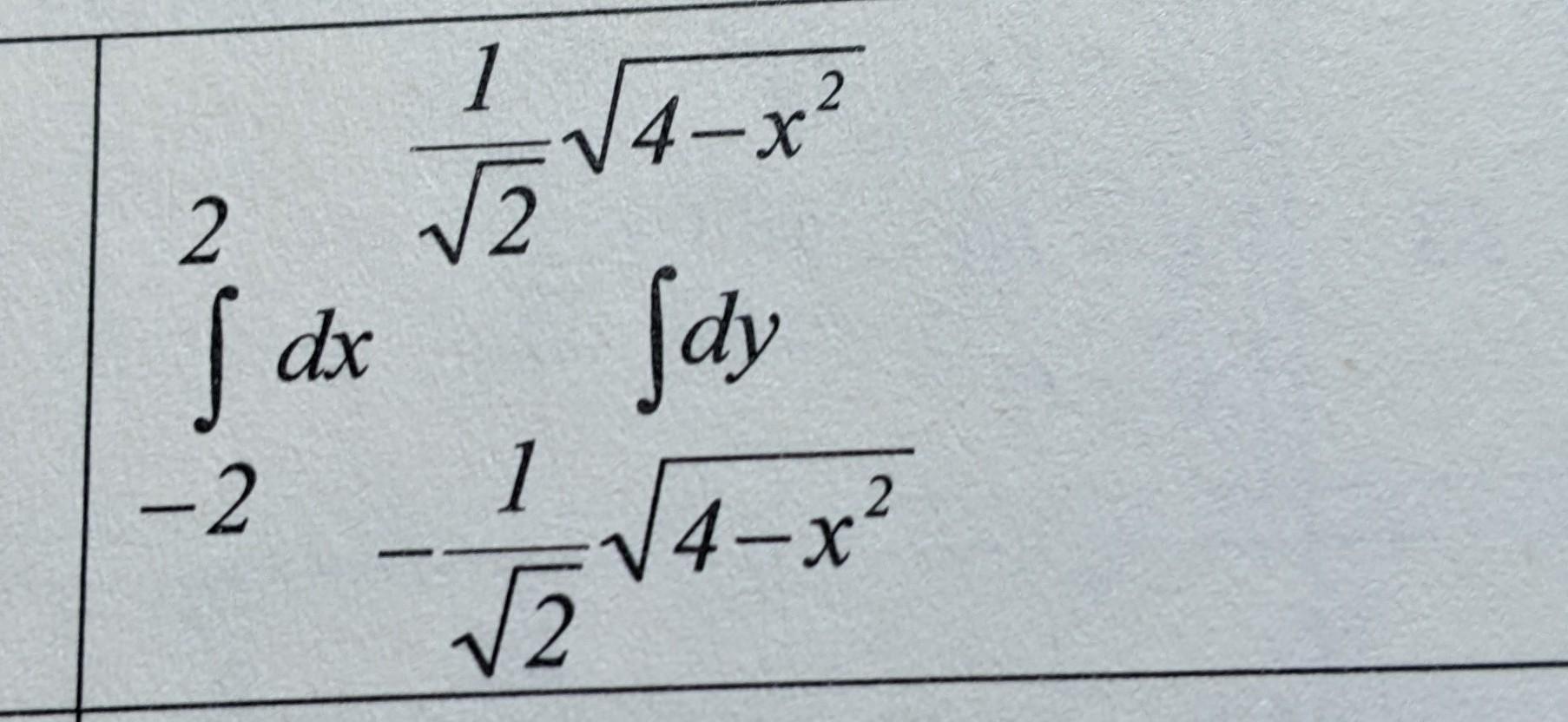
1 ответ

Посмотреть ответы

Megamozg

2205

Решение.
$\displaystyle \int\limits_{-2}^2\, dx\int\limits_{-\frac{\sqrt2}\sqrt}^{\frac{\sqrt2}\sqrt}\, dy$
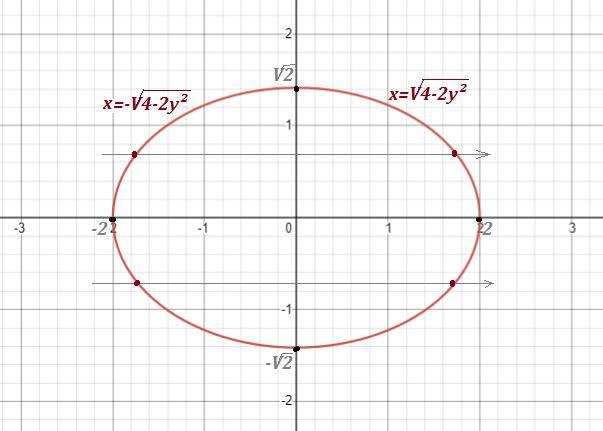
Область, по которой ведётся интегрирование - это эллипс с центром в точке (0,0) , большой полуосью a=2 и малой полуосью b=√2 . Действительно,
$y=\dfrac{\sqrt2}\cdot \sqrt\ \ \Rightarrow \ \ \ y^2=\dfrac\ \ ,\ \ 2y^2=4-x^2\ \ ,\ \ x^2+2y^2=4\ \Big|:4\ \Rightarrow$
$\dfrac+\dfrac=1$ - эллипс , центр (0,0) , а=2 , b=√2 .
Выразим переменную х .
$\dfrac=1-\dfrac\ \ ,\ \ x^2=4\cdot \dfrac\ \ ,\ \ x^2=2(2-y^2)\ \ ,\ \ x^2=4-2y^2\ ,\\\\x=\pm \sqrt$
Получили уравнения правой и левой половинок эллипса .
Поменяем порядок интегрирования .
$\displaystyle \int\limits_{-2}^2\, dx\int\limits_{-\frac{\sqrt2}\sqrt}^{\frac{\sqrt2}\sqrt}\, dy=\int\limits_{-\sqrt2}^{\sqrt2}\, dy\int\limits_{-\sqrt}^{\sqrt}\, dx=\int\limits_{-\sqrt2}^{\sqrt2}\, (\sqrt+\sqrt)\, dy=$

$\displaystyle =2\int\limits_{-\sqrt2}^{\sqrt2}\, \sqrt\, dy=2\sqrt2\int\limits_{-\sqrt2}^{\sqrt2}\, \sqrt\, dy=\\\\\\\bullet \int \sqrt\, dy=\Big[\ y=\sqrt2\, sint\ ,\ sint=\frac{\sqrt2}\ ,\ t=arcsin\frac{\sqrt2}\ ,\\\\\\dy=\sqrt2\, cost\, dt\ \Big]=\int \sqrt\cdot \sqrt2\, cost\, dt=2\cdot \int \sqrt\cdot cost\, dt=\\\\\\=2\int \sqrt\cdot cost\, dt=2\int cost\cdot cost\, dt=2\int cos^2t\, dt=2\int \frac\, dt=$

$\displaystyle =\int dt+\int cost\, dt=t+sint+C=arcsin\frac{\sqrt2}+\frac{\sqrt2}+C\ \ \bullet$

$\displaystyle =2\sqrt2\cdot \Big(arcsin\frac{\sqrt2}+\frac{\sqrt2}\Big)\Big|_{-\sqrt2}^{\sqrt2}=\\\\\\=2\sqrt2\cdot \Big(arcsin\frac{\sqrt2}{\sqrt2}+\frac{\sqrt2}{\sqrt2}-arcsin\frac{-\sqrt2}{\sqrt2}-\frac{-\sqrt2}{\sqrt2}\Big)=\\\\\\=2\sqrt2\cdot \Big(arcsin1+1+arcsin1+1\Big)=2\sqrt2\cdot (2arcsin1+2)=\\\\\\=2\sqrt2\cdot (2\cdot \frac{\pi }+2)=2\sqrt2\cdot (\pi +2)$

Хороший ответ

18 декабря 2022 15:20

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

диаметр окружности с центром точки а равен 6 см.расстояние между точками а и без равно 5см. точка D общая точка этих окружности. найдите диаметр окруж... На круговой диаграмме показано соотношение деревьев в парке. По данным диаграммы ответить на вопросы: а) сколько процентов составляют дубы в этом парк... Чему равно количество центнеров в 1 тонне 16 центнеров?... Какое число получится, если 75 умножить на 0,04?... решить задачу в гостиницу завезли 108 кроватей и 72 шкафа которые поровну разделили по номерам сколько номеров в гостинице если известно что их больше...