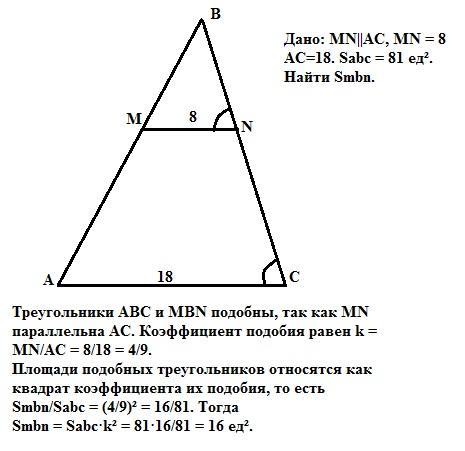
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно, АС-18,MN-8.Площадь треугольника АВС равна 81.Найдите площадь треугольника MBN

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
Smbn = 16 ед².
Объяснение:
Треугольники АВС и МBN подобны по двум углам, так как MN параллельна АС и ∠А = ∠М, как соответственные при параллельных прямых, а ∠В - общий. Тогда коэффициент подобия равен
k = MN/AC = 8/18 = 4/9.
Площади подобных треугольников относятся как квадрат коэффициента их подобия, то есть Smbn/Sabc = k² =(4/9)² =16/81. Тогда
Smbn = Sabc·k² = 81·16/81 = 16 ед².

Хороший ответ

19 декабря 2022 11:19

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Всякая ли фигура имеет центр симметрии ? Приведите пример .... Параллельные плоскости альфа и бета пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла в В1 и В2. Найти АА1 если... Даны стороны а и b треугольника и угол а между ними. Нарисуйте третью сторону треугольника, где: [3] a 8 см, c = 3√3 см, a = 120°.... Осевое сечение цилиндра квадрат,длина диагонали которого равна 20 см.Найдите радиус основания цилиндра... Найдите высоту треугольника ABC, опущенную на сторону BC, если стороны квадратных клеток равны 1....