ОЧЕНЬ НАДО! вычислите площадь фигуры, ограниченной линиями y=корень из x, y=1, x=4.с объяснением,пожалуйста )

1 ответ

Посмотреть ответы

Megamozg

2170

Ответ:
$\dfrac$ (кв. единица)
Объяснение:
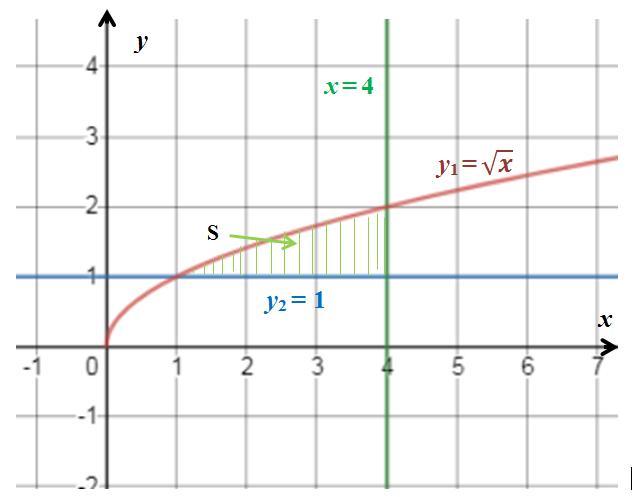
Фигура ограничена: сверху функцией y₁ = √x, справа x = 4, снизу прямой y₂ = 1 (см. рисунок). Находим точку пересечения функций y₁ и y₂:
y₁ = y₂ ⇔ √x = 1 ⇔ x = 1.
Площадь S фигуры вычислим с помощью определенного интеграла:
$\displaystyle S=\int\limits^ _ {(y_-y_ )} \, dx =\int\limits^ _ {(\sqrt -1)} \, dx =\int\limits^ _(x^\frac -1) \, dx = (\frac \cdot x^\frac-x) \left \ / {^_} \right.=\\\\= (\frac \cdot 4^\frac-4)-(\frac \cdot 1^\frac-1)=(\frac-4)-(\frac-1)=\frac-\frac-4+1=\frac-3=\frac.$

Хороший ответ

28 декабря 2022 10:09

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Построить график функции: y=(Log1/2х)+2... В группе туристов 20 человек. С помощью жребия они выбирают 3 человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, чт... Представьте в виде степени выражения 3.1... Найдите наименьшее значение x , удовлетворяющее системе неравенств { 5x + 15 ≤ 0, x + 5 ≥ 1.... 1)1+ cosx=2cos x/2 2)sinx=tg^2 x/2(1+cosx)Помогииите!:)))на Завтрааа...