1. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.2. Площадь прямоугольника (формулировка и доказательство).

3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника

1 ответ

Посмотреть ответы

Megamozg

2180

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

2.
Площадь прямоугольника равна произведению его смежных сторон:
S = ab.
Доказательство:
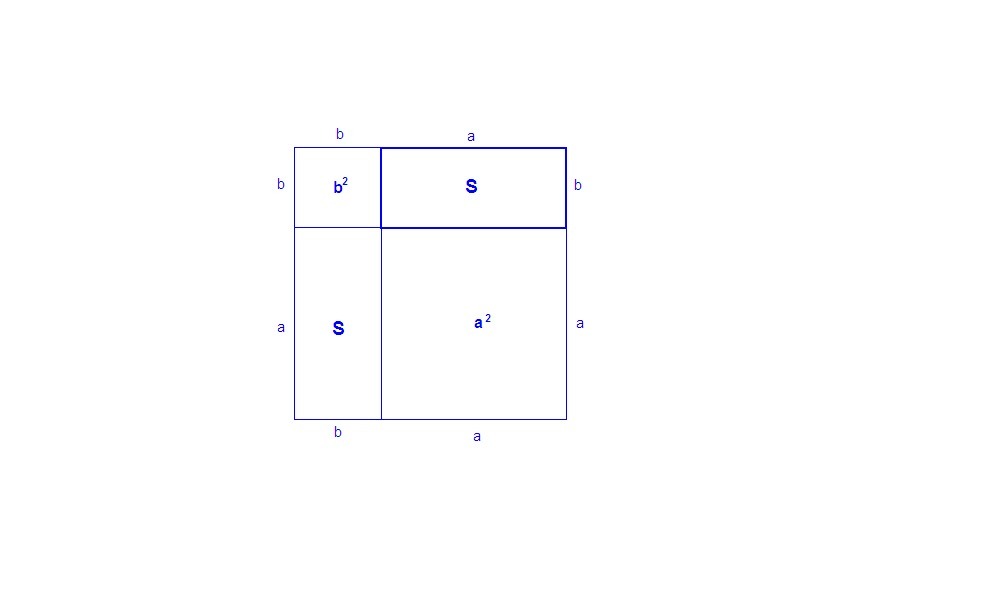
Достроим прямоугольник до квадрата со стороной (a + b).
Площадь квадрата равна квадрату его стороны:
Sкв = (a + b)²
Площадь квадрата равна сумме площадей фигур, составляющих его:
Sкв = a² + b² + 2S
a² + b² + 2S = (a + b)²
a² + b² + 2S = a² + b² + 2ab
2S = 2ab
S = ab.
Доказано.

3.
Если в четырехугольник можно вписать окружность, то суммы его противолежащих сторон равны. Значит, периметр четырехугольника равен 12 + 12 = 24 см.
Площадь любого многоугольника, в который можно вписать окружность вычисляется по формуле:
S = pr, где
р - полупериметр,
r - радиус вписанной окружности.
S = 24/2 · 5 = 12 · 5 = 60 см²

Хороший ответ

28 декабря 2022 12:15

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Треугольник CDE задан координатами своих вершин: C(2; 2), D(6;5), E(5; -2) А) Докажите, что треугольник CDE-равнобедренный. Б) Найдете бесектрису, пр... ab=18 r=? угол c=150 градусо тогда дуга ab=..... помогите пж... Основанием пирамиды служит квадрат со стороною 16см. Найдите объём пирамиды, если каждое её боковое ребро наклонено к основанию пирамиды под углом 45°... треугольник abc вписан в окружность с центром o. .найдите градусную меру угла c треугольника abc,если угол aob равен 73градусса... Угол В при основании ВС равнобедренного треугольника АВС равен 80°. Биссектриса угла, смежного с углом АВС, пересекает луч АС в точ- ке F, а точка...