Площадь боковой поверхности правильной четырехугольной призмы равна Q.Сечение призмы,проходящее через диагональ нижнего основания и противолезащую вершину верхнего основания ,образует с плоскостью основания призмы угол фльфа .Найти площадь сечения.сделайте рисунок и поробное объяснение. решение из интернета а также решение провессора Рензи не переписывайте.

1 ответ

Посмотреть ответы

Megamozg

2200

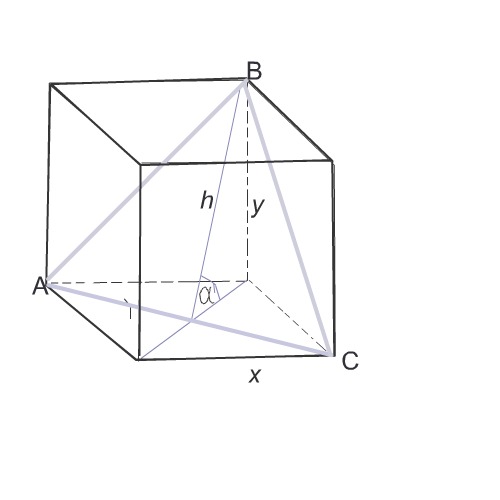
Площадь сечения этой призмы - равнобедренный треугольник.
Его боковые стороны АВ и ВС диагонали боковых граней,
основание - диагональ d квадрата, лежащего в основании призмы.

Пусть ребро основания х, боковое ребро у.
Диагональ основания по формуле диагонали квадрата
d=х√2
Высота сечения h
sinα=у:h
h=у:sinα

Sсеч=½·h·d
Sсеч=½·х√2*у:sinα
Sсеч= ½·ху√2:sinα
Площадь одной грани
ху=Q:4
Sсеч=½ ·Q:4 √2 : sinα= ⅛ Q√2:sinα

Хороший ответ

28 декабря 2022 15:12

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В выпуклом четырёхугольнике ABCD известно что AB=BC AD=CD B=44 градусов D=128 градусов найдите угол A запишите решения и ответ... Чему равен корень из 48?... Высота прямоугольного треугольника, проведённая из вершины прямого угла, бежит гипотенузу на отрезки 45 см и 5 см. Найдите: а) высоту, б) катеты треуг... В треугольнике ABC AB=BC=65 , AC=50 . Найдите длину медианы BM .... На отрезке AB выбрана точка C так, что AC=60 и BC=5 . Построена окружность с центром , проходящая через C. Найдите длину отрезка касательной, проведён...