1)сформулируйте и докажите теорему о разложении вектора по двум не коллинеАрным векторам . 2)объясните,как вводится прямоугольная система координат.

Рассмотрим векторы на плоскости. Для этого введем прямоугольную (декартову) систему координат. Она вводится так: на плоскости берут произвольную точку О и от нее проводят взаимно перпендикулярные прямые - оси координат, причем вправо от этой точки координаты (точки, лежащие на оси) имеют положительное значение, а влево - отрицательные.
Отложим по оси Х вектор "i", а по оси Y - вектор "j". Эти вектора ортогональны, то есть взаимно перпендикулярны. Они называются координатными векторами или ортами и образуют БАЗИС на плоскости. Базис и начало координат задают плоскость, на которой располагаются вектора. ЛЮБОЙ вектор "р" на этой плоскости можно выразить ЕДИНСТВЕННЫМ образом через координатные вектора в виде р=k*i+n*j, где "k" и "n" - числа, которые называются координатами вектора "р" в данном базисе, причем "i" и "j" нельзя менять местами.
Выражение р=k*i+n*j (1) называется разложением вектора "р"
по базису (i;j). Вектор "р" можно обозначить и так: р=(k*i;n*j).
Причем базисные (координатные) вектора не обязательно (и это важно) равны.
Если вектор записан в виде р=x*a+y*b (2), где "а" и "b" -неколлинеарные вектора, то можно сказать, что вектор "р" разложен по векторам "а" и "b". А вектора "а" и "b" - являются базисом. (Сравним выражения (1) и (2)).
Теорема: "Любой вектор "р" можно разложить,и притом единственным образом,по двум данным неколлинеарным векторам "a" и "b", причем коэффициенты этого разложения "x" и "y" определяются единственным образом".
Доказательство: в прямоугольной системе координат отложим векторы
"а"=, "b"= и "р"=.
Запишем равенство (2) в координатах вектора "р":
р1=x*a1+y*b1 (3) и
p2=х*а2+y*b2 (4). Из уравнения (4) коэффициент "y" определяется через коэффициент х единственным способом, так как уравнение линейное. Подставляя затем значение коэффициента "y" в уравнение (3), получим и единственное значение для коэффициента "х". Следовательно, для уравнения (2) существует единственная, удовлетворяющая ему, пара чисел "х" и "y".
Теорема доказана.
Итак, чтобы разложить данный нам вектор "р" с координатами "р1" и "р2", по двум неколлинеарным (не параллельным) векторам а и b, необходимо решить систему уравнений:
р1=x*а1+y*b1 и
р2=x*a2+yb2 относительно коэффициентов х и y.
Получим запись для вектора "р" в виде р = x*a+y*b.

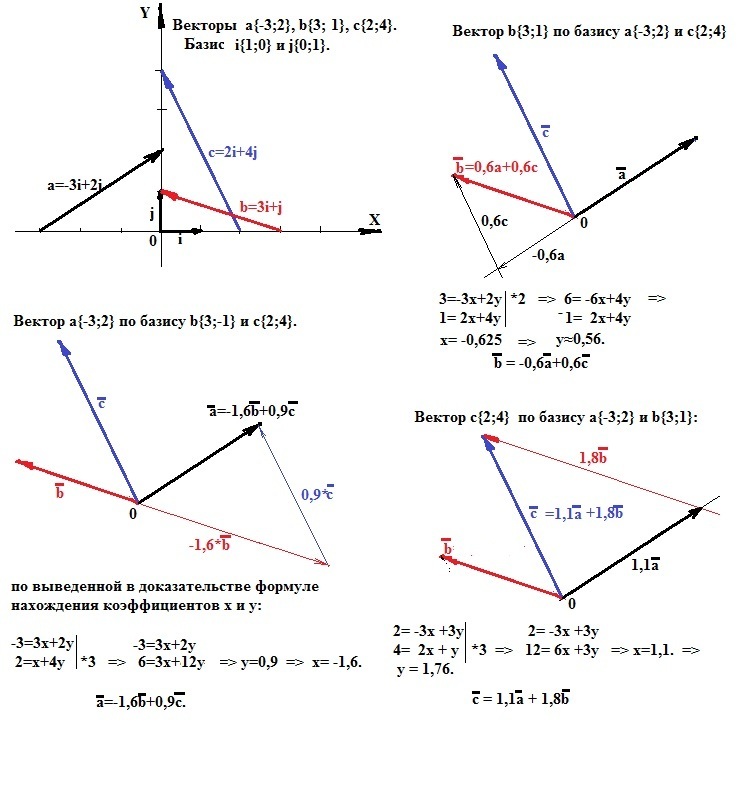
Рассмотрим разложение вектора по двум неколлинеарным векторам на конкретном примере (смотри приложение).